
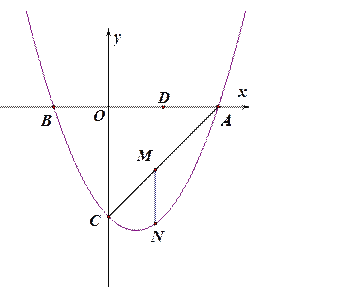
【题目】如图,抛物线![]() 与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于
与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于![]() 轴,交AC于点M.
轴,交AC于点M.
(1) 求直线AC的解析式;
(2)当点N运动至抛物线的顶点时,求此时MN的长;
(3)设点N的横坐标为t,MN的长度为l;
①求l与t之间的函数关系式,并写出t的取值范围;
②l是否存在最值,有如有写出最值;
(4)点D是点B关于![]() 轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?
轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?
若存在,请求出此时△CAN的面积;若不存在,请说明理由.
【答案】(1)y=x-4;(2)当t=2时,l有最大值2,此时N(2,2);(3)存在,点M的坐标为(2,﹣2),(1,-3),![]() =4或3.
=4或3.
【解析】试题分析:(1)设直线AC的解析式为y=kx+b,过A(4,0)、C(0,-4)两点,即可求得k、b的值,从而求得直线AC的解析式;(2)求得抛物线的顶点坐标及当x=1时点M的坐标,即可求得MN的长;(3)①设![]() ,根据MN=(t-4)-(
,根据MN=(t-4)-(![]() ),化简即可求得l与t之间的函数关系式,根据图象直接写出x的取值范围即可;②存在,分DO=DM、MO=MD和MO=OD(这种情况不存在)三种情况讨论求解即可,第三种情况不存在,可以不写.
),化简即可求得l与t之间的函数关系式,根据图象直接写出x的取值范围即可;②存在,分DO=DM、MO=MD和MO=OD(这种情况不存在)三种情况讨论求解即可,第三种情况不存在,可以不写.
试题解析:
(1)∵抛物线的解析式为:![]()
![]()
∴A(4,0)C(0,-4)
∵![]() 过A,C两点
过A,C两点
∴![]()
![]()
(2)∵抛物线的解析式为:![]() 顶点坐标为(1,
顶点坐标为(1,![]() )
)
直线AC的解析式y=x-4,当x=1时,M(1,-3)
∴MN=![]()
(3)①∵![]()
∴![]() ( 4≤t≤0)
( 4≤t≤0)
![]() ,
,
∴当t=2时,l有最大值2,此时N(2,2)
(3)存在.
∵点B(-2,0),
∴点D是点B关于y轴的对称点,∴点D(2,0))
在△ODM中,

(ⅰ)若DO=DM,
∵A(4,0),D(2,0),∴AD=OD=DM=2。
又在Rt△AOC中,OA=OC=4,
∴∠OAC=45°。∴∠DMA=∠OAC=45°。
∴∠ADM=90°。此时,点M的坐标为(2,﹣2)。
![]()
![]()

(ⅱ)若MO=MD,过点M作MH⊥x轴于点H。
由等腰三角形的性质得:OH=OD=1,∴AH=3,
∴在等腰直角△AHM中,HM=AH=3,
∴M(1,-3)
![]()
![]()
综上所述,使得△ODM是等腰三角形,所求点M的坐标为:(2,﹣2),(1,-3), △CAN的面积为4或3.


科目:初中数学 来源: 题型:
【题目】如图,已知AD=AE ,添加下列条件仍无法证明△ABE≌△ACD的是( )

A. AB=AC B. BE=CD C. ∠B=∠C D. ∠ADC=∠AEB
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=AC,AB的垂直平分线交AB于D,交AC于E,BE恰好平分△ABC,有以下结论:(1)ED=EC;(2)△BEC的周长等与2AE+EC;(3)图中共有3个等腰三角形;(4)∠A=36°,其中正确的共有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:如图①,在△ABC中,AB=AC,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,AE,求证:△ACE≌△CBD.
应用:如图②,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G,求∠CGE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答一个问题后,将结论作为条件之一,提出与原问题有关的新问题,我们把它称为原问题的一个“逆向”问题.例如,原问题是“若矩形的两边长分别为3和4,求矩形的周长”,求出周长等于14后,它的一个“逆向”问题可以是“若矩形的周长为14,且一边长为3,求另一边的长”;也可以是“若矩形的周长为14,求矩形面积的最大值”,等等.
(1)设A=![]() ,B=
,B=![]() ,求A与B的积;
,求A与B的积;
(2)提出(1)的一个“逆向”问题,并解答这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,有一个长方体,它的长、宽、高分别为5cm,3cm,4cm.在顶点A处有一只蚂蚁,它想吃到与顶点A相对的顶点B的食物.
(1)请画出该蚂蚁沿长方体表面爬行的三条线路图(即平面展开图);
(2)已知蚂蚁沿长方体表面爬行的速度是1cm/s,问蚂蚁能否在8秒内获取到食物?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com