
����Ŀ�����һ�������������Ϊ����֮һ�������ԭ�����йص������⣬���ǰ�����Ϊԭ�����һ�������������⣮���磬ԭ�������������ε����߳��ֱ�Ϊ3��4������ε��ܳ���������ܳ�����14������һ��������������������������ε��ܳ�Ϊ14����һ�߳�Ϊ3������һ�ߵij�����Ҳ�������������ε��ܳ�Ϊ14���������������ֵ�����ȵȣ�
��1����A=![]() ��B=
��B=![]() ����A��B�Ļ���
����A��B�Ļ���
��2�������1����һ�������������⣬�����������⣮
 �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
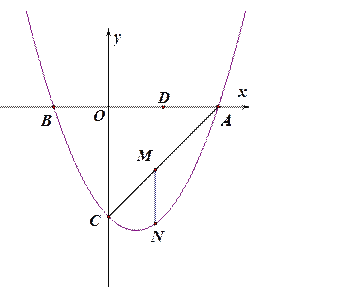
����Ŀ����ͼ��������![]() ��y�ύ�ڵ�C����x�ύ�ڵ�A�͵�B����N����AC����ֱ���·����������ϵ�һ�����㣬����N��MNƽ����
��y�ύ�ڵ�C����x�ύ�ڵ�A�͵�B����N����AC����ֱ���·����������ϵ�һ�����㣬����N��MNƽ����![]() �ᣬ��AC�ڵ�M��
�ᣬ��AC�ڵ�M��
(1) ��ֱ��AC�Ľ���ʽ��
��2������N�˶��������ߵĶ���ʱ�����ʱMN�ij���
��3�����N�ĺ�����Ϊt��MN�ij���Ϊl��
����l��t֮��ĺ�����ϵʽ����д��t��ȡֵ��Χ��
��l�Ƿ������ֵ��������д����ֵ��
��4����D�ǵ�B����![]() ��ĶԳƵ㣮���������Ƿ��е�N��ʹ��ODM�ǵ��������Σ�
��ĶԳƵ㣮���������Ƿ��е�N��ʹ��ODM�ǵ��������Σ�
�����ڣ��������ʱ��CAN��������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס�������������ͬһ·�ߴ�A��ǰ��B�أ�����![]() ǧ��/ʱ���ٶ�������ʻ��;�г��ֹ��Ϻ�ͣ��ά�ޣ��ú���
ǧ��/ʱ���ٶ�������ʻ��;�г��ֹ��Ϻ�ͣ��ά�ޣ��ú���![]() ǧ��/ʱ���ٶȼ�����ʻ�����ڼ׳���2Сʱ������ǰ��B�أ��ȼ���30���ӵ������B�غ��Ұ�ԭ�ٶȷ���A�أ�����
ǧ��/ʱ���ٶȼ�����ʻ�����ڼ׳���2Сʱ������ǰ��B�أ��ȼ���30���ӵ������B�غ��Ұ�ԭ�ٶȷ���A�أ�����![]() ǧ��/ʱ���ٶȷ���A�أ���ס���������A�����s��ǧ�ף����׳��뿪A�ص�ʱ��Ϊt��ʱ����s��t֮��ĺ���ͼ����ͼ��ʾ��
ǧ��/ʱ���ٶȷ���A�أ���ס���������A�����s��ǧ�ף����׳��뿪A�ص�ʱ��Ϊt��ʱ����s��t֮��ĺ���ͼ����ͼ��ʾ��
��1����![]() ��ֵ��
��ֵ��
��2����׳�ά������ʱ�䣮
��3����������;�еڶ�������ʱt��ֵ��
��4����ֱ��д�����������40ǧ��ʱ��t��ֵ��ȡֵ��Χ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a<b�������й�ϵʽ���������ǣ� ��
A.4a<4bB.4a4bC.a+4<b+4D.a��4<b��4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB=AC��AD=AE����BAC=��DAE=����BE��AC��CD�ֱ��ཻ�ڵ�N��M.
��1����֤��BE=CD��
��2�����BMC�Ĵ�С.���æ���ʾ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P�ǡ�MAN�Ľ�ƽ������һ�㣬PB��AM��B��PC��AN��C.
��1����ͼ1����D��E�ֱ����߶�AB��AC�ϣ��ҡ�DPE=![]() ��BPC����֤��DE=BD+CE��
��BPC����֤��DE=BD+CE��

��2����ͼ2����D��AB���ӳ����ϣ�E��ֱ��AC�ϣ���DE��BD��CE���ߵ�������ϵ�仯�����仯����ֱ��д�����ۼ��ɡ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й������ġ�һ��һ·�����й�������Ļ�����Ӯ֮·����ͳ�ƣ���һ��һ·���������ǵ����˿�ԼΪ44���ˣ���44�ڡ�������ÿ�ѧ�������ɱ�ʾΪ��������
A.4.4��107B.4.4��108C.4.4��109D.0.44��1010
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com