
【题目】探究:如图①,在△ABC中,AB=AC,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,AE,求证:△ACE≌△CBD.
应用:如图②,在菱形ABCF中,∠ABC=60°,延长BA至点D,延长CB至点E,使BE=AD,连结CD,EA,延长EA交CD于点G,求∠CGE的度数.

【答案】探究:证明见试题解析;应用:∠CGE=60°.
【解析】试题分析:探究:由AB=AC,∠ABC=60°,得到△ABC是等边三角形,从而有BC=AC,∠ACB=∠ABC,由BE=AD,得到CE=BD,即可得到△ACE≌△CBD;
应用:如图,连接AC,易知△ABC是等边三角形,由探究可知△ACE≌△CBD,得到∠E=∠D,由∠BAE=∠DAG,得到∠CGE=∠ABC,由∠ABC=60°,即可得到结论.
试题解析:探究:∵AB=AC,∠ABC=60°,∴△ABC是等边三角形,∴BC=AC,∠ACB=∠ABC,∵BE=AD,∴BE+BC=AD+AB,即CE=BD,在△ACE和△CBD中,∵CE=BD,∠ACB=∠ABC,BC=AC,∴△ACE≌△CBD(SAS);
应用:如图,连接AC,易知△ABC是等边三角形,由探究可知△ACE≌△CBD,∴∠E=∠D,∵∠BAE=∠DAG,∴∠E+∠BAE=∠D+∠DAG,∴∠CGE=∠ABC,∵∠ABC=60°,∴∠CGE=60°.



 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D为BC延长线上的一点,以AD为边向形外作等边△ADE,连接CE.(1) 求证:△ACE≌△ABD;
(2) 在点D运动过程中,∠DCE的度数是否发生变化?若不变化,求它的度数;若变化,说明理由;
(3) 若∠BAE=150°,△ABD的面积为6,求四边形ACDE的面积.
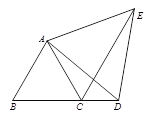
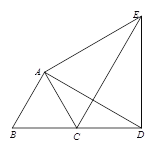
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有红、黄、蓝三种颜色的球(除颜色外其余都相同),
其中红球有1个,蓝球有1个,现从中任意摸出一个是红球的概率为![]() .
.
(1)求袋中黄球的个数.
(2)第一次摸出一个球(放回),第二次再摸一个球,请用画树状图或列表法求两次摸到都是红球的概率.
(3)若规定每次摸到红球得5分,每次摸到黄球得3分,每次摸到蓝球得1分,小芳摸6次球(每次摸1个球,摸后放回)合计得20分,请直接写出小芳有哪几种摸法?(不分球颜色的先后顺序)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于
与y轴交于点C,与x轴交于点A和点B.若N点是AC所在直线下方该抛物线上的一个动点,过点N作MN平行于![]() 轴,交AC于点M.
轴,交AC于点M.
(1) 求直线AC的解析式;
(2)当点N运动至抛物线的顶点时,求此时MN的长;
(3)设点N的横坐标为t,MN的长度为l;
①求l与t之间的函数关系式,并写出t的取值范围;
②l是否存在最值,有如有写出最值;
(4)点D是点B关于![]() 轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?
轴的对称点.抛物线上是否有点N,使△ODM是等腰三角形?
若存在,请求出此时△CAN的面积;若不存在,请说明理由.
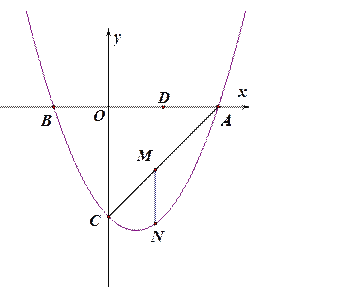
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两辆汽车沿同一路线从A地前往B地,甲以![]() 千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以
千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以![]() 千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以
千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,比甲早30分钟到达.到达B地后,乙按原速度返回A地,甲以![]() 千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
千米/时的速度返回A地.设甲、乙两车与A地相距s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
(1)求![]() 的值.
的值.
(2)求甲车维修所用时间.
(3)求两车在途中第二次相遇时t的值.
(4)请直接写出当两车相距40千米时,t的值或取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB=AC,AD=AE,∠BAC=∠DAE=α,BE与AC、CD分别相交于点N、M.
(1)求证:BE=CD;
(2)求∠BMC的大小.(用α表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲、乙两公司合做,12天可以完成,共需付工费102000元;如果甲、乙两公司单独完成此项公程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1500元。
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com