练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】抛物线y=x2 ， 当﹣1≤x≤3时，y的取值范围是（ ）
    A.﹣1≤y≤9
    B.0≤y≤9
    C.1≤y≤9
    D.﹣1≤y≤3

    【答案】B
    【解析】解：
    ∵y=x2 ，
    ∴抛物线开口向上，对称轴为y轴，
    ∴当﹣1≤x≤0时，y随x的增大而减小，故当x=﹣1时，y有最大值1，当x=0时，y有最小值0；
    当0≤x≤3时，y随x的增大而增大，故当x=3时，y有阳大值9，当x=0时，y有最小值0；
    ∴当﹣1≤x≤3时，y的取值范围是0≤y≤9，
    故答案为：B．
    由抛物线开口方向、对称轴及增减性求得其最大和最小值即可求得答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】下表所列为某商店薄利多销的情况，某商品原价为560元，随着不同幅度的降价，日销量（单位为件）发生相应的变化．如果售价为500元时，日销量为（ ）件．

    降价（元）

    5

    10

    15

    20

    25

    30

    35

    日销量（件）

    780

    810

    840

    870

    900

    930

    960


    A.1200
    B.750
    C.1110
    D.1140

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1）在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于点D，BE⊥MN于点E．

    (1)求证： DE=AD+BE．

    (2)当直线MN绕点C旋转到图2的位置时，DE、AD、BE又怎样的关系？请直接写出你的结论，不必说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】据报道，春节期间微信红包收发高达3270000000次，数字3270000000用科学记数法表示为 _____

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在□ABCD中，分别以AB、AD为边向外作等边△ABE，△ADF，延长CB交AE于点G，点G落在点A、E之间，连接EF、CF．则以下四个结论：①CG⊥AE；②△CDF≌△EBC；③∠CDF =∠EAF；④△ECF是等边三角形．其中一定正确的是 ．（把正确结论的序号都填上）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】64的立方根是（　　）

    A. 8 B. 4 C. ﹣8 D. ±8

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】抛物线y=﹣x2不具有的性质是（ ）
    A.开口向上
    B.对称轴是y轴
    C.在对称轴的左侧，y随x的增大而增大
    D.最高点是原点

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线y=﹣x+3交y轴于点A，交x轴与点B，抛物线y=﹣x2+bx+c经过点A和点B，点P为抛物线上直线AB上方部分上的一点，且点P的横坐标为t，过P作PE∥x轴交直线AB于，作PH⊥x轴于H，PH交直线AB于点F．

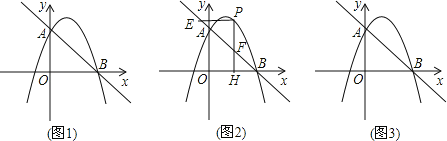
    （1）求抛物线解析式；

    （2）若PE的长为m，求m关于t的函数关系式；

    （3）是否存在这样的t值，使得∠FOH﹣∠BEH=45°？若存在，求出t值，并求tan∠BEH的值，若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次函数y=x+3的图象不经过( )

    A. 第一象限B. 第二象限C. 第三象限D. 第四象限

    查看答案和解析>>

    同步练习册答案