
【题目】如图,在□ABCD中,分别以AB、AD为边向外作等边△ABE,△ADF,延长CB交AE于点G,点G落在点A、E之间,连接EF、CF.则以下四个结论:①CG⊥AE;②△CDF≌△EBC;③∠CDF =∠EAF;④△ECF是等边三角形.其中一定正确的是 .(把正确结论的序号都填上)

【答案】②③④
【解析】
试题分析:在ABCD中,∠ADC=∠ABC,AD=BC,CD=AB, ∵△ABE、△ADF都是等边三角形,
∴AD=DF,AB=EB,∠ADF=∠ABE=60°, ∴DF=BC,CD=BC, ∴∠CDF=360°-∠ADC-60°=300°-∠ADC,
∠EBC=360°-∠ABC-60°=300°-∠ABC, ∴∠CDF=∠EBC, ∴△CDF≌△EBC(SAS),故②正确;
在ABCD中,∠DAB=180°-∠ADC, ∴∠EAF=∠DAB+∠DAF+∠BAE=180°-∠ADC+60°+60°=300°-∠ADC,
∴∠CDF=∠EAF,故③正确;
同理可证△CDF≌△EAF,∴EF=CF, ∵△CDF≌△EBC, ∴CE=CF, ∴EC=CF=EF,
∴△ECF是等边三角形,故④正确;
当CG⊥AE时,∵△ABE是等边三角形, ∴∠ABG=30°, ∴∠ABC=180°-30°=150°,
∵∠ABC=150°无法求出,故①错误;


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】用28米长的铁丝围成一个一边靠墙的长方形。

(1)当垂直于墙的一边比另一边少7米时,求长方形的面积。
(2)按下表中列出的数据要求,填写表格。

观察表格,你感到长方形的面积会不会有最大的情况?如果会,可能是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分5分)画图并填空:
如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点C的对应点C′.
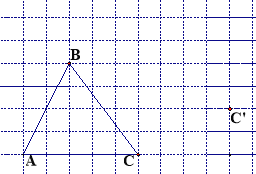
(1)画出平移后的△A′B′C′,(利用网格点和三角板画图)
(2)画出AB边上的高线CD;
(3)画出BC边上的中线AE;
(4)在平移过程中高CD扫过的面积为 .(网格中,每一小格单位长度为1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线DE交BC于D,交AB于E,F在DE上,且AF∥CE.
(1)说明四边形ACEF是平行四边形;(2)当∠B满足什么条件时,四边形ACEF是菱形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=∠B=∠C=90°,请你再添加一个条件,使该四边形是正方形,你添加的条件是__________.(填写其中一种情况即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC的周长为21cm,AB=6cm,BC边上中线AD=5cm,△ACD周长为16cm,则AC的长为__________cm.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com