
【题目】如图,直线y=﹣x+3交y轴于点A,交x轴与点B,抛物线y=﹣x2+bx+c经过点A和点B,点P为抛物线上直线AB上方部分上的一点,且点P的横坐标为t,过P作PE∥x轴交直线AB于,作PH⊥x轴于H,PH交直线AB于点F.
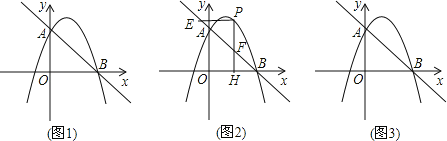
(1)求抛物线解析式;
(2)若PE的长为m,求m关于t的函数关系式;
(3)是否存在这样的t值,使得∠FOH﹣∠BEH=45°?若存在,求出t值,并求tan∠BEH的值,若不存在,请说明理由.
【答案】(1)抛物线解析式为y=﹣x2+2x+3;(2)m与t的关系式为m=﹣t2+3t;(3)存在满足条件的t的值,t的值为1,tan∠BEH的值为![]() .
.
【解析】
试题分析:(1)由直线AB的解析式可求得A、B两点的坐标,代入抛物线解析式可求得b、c,可求得抛物线解析式;
(2)由P点坐标表示出E点的纵坐标,代入直线AB解析式,可求得E点横坐标,则可用t表示出PE的长,可得到m关于t的函数关系式;
(3)过E作EG⊥x轴于点G,则可用t表示出GH和EG,由三角形外角的性质和已知条件可证得∠EHG=∠FOH,可证明△FOH∽△EHG,根据相似三角形的性质可求得t的值,则可求得tan∠EHG,结合∠BEH=∠FOH﹣45°,则可求得tan∠BEH的值.
解:(1)在直线y=﹣x+3中,令x=0可得y=3,令y=0可得x=3,
∴A(0,3),B(3,0),
∵抛物线y=﹣x2+bx+c过A、B两点,
∴把A、B两点的坐标代入可得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=﹣x2+2x+3;
(2)∵P点在抛物线上,
∴P点坐标为(t,﹣t2+2t+3),
∵PE∥x轴,
∴E点纵坐标为﹣t2+2t+3,
∵E点在直线AB上,
∴把E点纵坐标代入直线AB解析式可得﹣t2+2t+3=﹣x+3,解得x=t2﹣2t,
∴E点横坐标为t2﹣2t,
∴PE=m=t﹣(t2﹣2t)=﹣t2+3t,
∴m与t的关系式为m=﹣t2+3t;
(3)如图,过E作EG⊥x轴于点G,
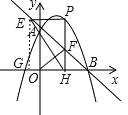
∵OA=OB=3,
∴∠EBO=45°,
∴∠EHG=∠BEH+∠EBO=∠EBH+45°,
∵∠FOH﹣∠BEH=45°,
∴∠FOH=∠BEH+45°,
∴∠EHG=∠FOH,且∠FHO=∠EGH=90°,
∴△FOH∽△EGH,
∴![]() =
=![]() ,
,
∵OH=t,F在直线AB上,
∴FH=﹣t+3,
由(2)可知EG=﹣t2+2t+3,GH=m=﹣t2+3t,
∴![]() =
=![]() ,解得t=1,
,解得t=1,
∴OH=1,FH=2,
∴tan∠FOH=![]() =2,
=2,
∵∠FOH﹣∠BEH=45°,
∴∠BEH=∠FOH﹣45°,
∴tan∠BEH=tan(∠FOH﹣45°)=![]() =
=![]() =
=![]() ,
,
综上可知存在满足条件的t的值,t的值为1,tan∠BEH的值为![]() .
.


科目:初中数学 来源: 题型:
【题目】下列调查中,适合全面调查方式的是( )
A. 调查全国人民的环保意识 B. 调查中秋节期间市场月饼的质量
C. 调查某班40名同学的体重 D. 调查某类烟花爆炸燃放安全质量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=∠B=∠C=90°,请你再添加一个条件,使该四边形是正方形,你添加的条件是__________.(填写其中一种情况即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阜阳某企业今年1月份产值为a万元,2月份比1月份减少了10%,预计3月份比2月份增加15%.则3月份的产值将达到( )
A. (a﹣10%)(a+15%)万元 B. (a﹣10%+15%)万元
C. a(1﹣10%)(1+15%)万元 D. a(1﹣10%+15%)万元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com