
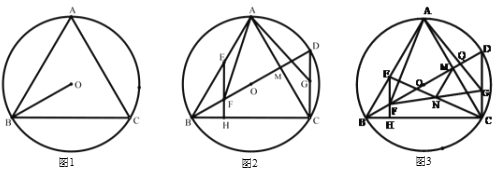
【题目】已知:![]() 内接于
内接于![]() ,
,![]() ,
,![]() 平分
平分![]() .
.
(1)如图,求证:![]() 为等边三角形.
为等边三角形.
(2)如图,![]() 为
为![]() 直径,点
直径,点![]() 在
在![]() 上,
上,![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,将
,将![]() 绕点
绕点![]() 逆时针旋转使点
逆时针旋转使点![]() 落在
落在![]() 上的点
上的点![]() 处,求证:
处,求证:![]() ;
;
(3)如图,在(2)的条件下,![]() 与
与![]() 交于点
交于点![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,若
,若![]() 的面积
的面积![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接OA、OC,证明ΔOABΔOBC,根据等边三角形的性质可得AB=BC,又因AB=AC,即可判定ΔABC为等边三角形;(2)过点A作AL⊥CD于L,根据等边三角形的性质可得BD⊥AC,∠ABM=30°,再求得∠ACL=30°,即可判定ΔABMΔACL,由全等三角形的性质可得BM=CL, AM=AL ,再证明RtΔAFMRtΔAGL,即可得FM=GH,由此可得BM-FM=CL-GL,即BF=CG;(3)延长CD至S使得DS=DA,易证ΔADS为等边三角形,即可证得DQ![]() AS,由平行线分线段成比例定理可得AQ:QG=SD:DG=5:3,即可得到DA:DG=5:3;设DA=DC=5k,DG=3k,则CG=BF=2k;计算得
AS,由平行线分线段成比例定理可得AQ:QG=SD:DG=5:3,即可得到DA:DG=5:3;设DA=DC=5k,DG=3k,则CG=BF=2k;计算得![]() ,所以
,所以![]() ,
,![]() ;再证明ΔABFΔACG,可得∠BAF=∠CAG,所以∠FAG=∠FAC+∠CAG=∠FAC+∠BAF=60°,即可判定ΔAFG是等边三角形;在
;再证明ΔABFΔACG,可得∠BAF=∠CAG,所以∠FAG=∠FAC+∠CAG=∠FAC+∠BAF=60°,即可判定ΔAFG是等边三角形;在![]() 中,
中,![]() ,解
,解![]() 得
得![]() ;由
;由![]() ,所以
,所以![]() ;又因
;又因![]() ,可得
,可得![]() ;由(2)知
;由(2)知![]() ,可判定
,可判定![]() ,可得
,可得![]() ;再求得
;再求得![]() ,所以等边
,所以等边![]() 的面积
的面积![]() ,解得
,解得![]() ,所以
,所以![]()
(1)证明:连接![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
,
又∵![]() 平分
平分![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 为等边三角形;
为等边三角形;

(2)过点![]() 作
作![]() 于
于![]() ,
,
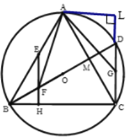
∵![]() 平分
平分![]() ,
,
∴![]() ,
, ![]() ,
,
∵![]() 是直径,
是直径,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ;
;
(3)延长![]() 至
至![]() 使得
使得![]() ,
,

易证![]() 为等边
为等边![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
设![]() ,
,
则![]() ,
,
计算得![]() ,
,
∴![]() ,
,![]() ,
,
再证明![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形;
为等边三角形;
在![]() 中,
中,![]()
解![]() 得
得![]()
∵![]()
∴![]()
又∵![]()
∴可证![]()
由(2)知![]()
∴![]()
∴![]()
又∵![]()
∴![]()
等边![]() 的面积
的面积![]()
∴![]()
∴![]()
∴![]()


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
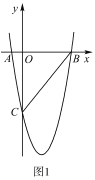
【题目】如图![]() ,在平面直角角坐标系中,已知抛物线
,在平面直角角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的函数表达式;
(2)如图![]() ,
,![]() 轴与抛物线相交于点
轴与抛物线相交于点![]() ,点
,点![]() 是直线
是直线![]() 下方抛物线上的动点,过点
下方抛物线上的动点,过点![]() 且与
且与![]() 轴平行的直线与
轴平行的直线与![]() ,
,![]() 分别交于点
分别交于点![]() 试探究当点
试探究当点![]() 运动到何处时,线段
运动到何处时,线段![]() 的最长,求点
的最长,求点![]() 的坐标;
的坐标;
(3)若点![]() 为抛物线的顶点,点
为抛物线的顶点,点![]() 是该抛物线上的一点,在
是该抛物线上的一点,在![]() 轴、
轴、![]() 轴上分别找点
轴上分别找点![]() ,使四边形
,使四边形![]() 的周长最小,请求出点
的周长最小,请求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+2与x轴、y轴分别交于点A(-1,0)和点B,与反比例函数y=![]() 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n).
(1)求k的值;
(2)求反比例函数的解析式;
(3)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线AB和双曲线y=![]() 交于点P、Q,且PQ=2QD,求点D的坐标.
交于点P、Q,且PQ=2QD,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗。我市某食品厂为了解市民对去年销量较好的肉馅粽(咸)、豆沙馅粽(甜)、红枣馅粽(甜)、蛋黄馅粽(咸)(以下分别用![]() 表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整)。请根据以上信息回答:
表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整)。请根据以上信息回答:
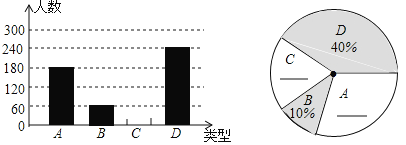
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有7000人,请估计爱吃A粽的人数;
(4)若有外型完全相同的![]() 粽各一个,煮熟后,小王吃了两个。用列表或画树状图的方法,求他吃到的两个粽子都是甜味的概率。
粽各一个,煮熟后,小王吃了两个。用列表或画树状图的方法,求他吃到的两个粽子都是甜味的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,(
,(![]() 左
左![]() 右),交y轴于点C,△AOC的周长为12,sin∠CBA=
右),交y轴于点C,△AOC的周长为12,sin∠CBA=![]() ,则下列结论:①A点坐标(-3,0);②a=
,则下列结论:①A点坐标(-3,0);②a=![]() ;③点B坐标(8,0);④对称轴x=
;③点B坐标(8,0);④对称轴x=![]() .其中正确的有( )个.
.其中正确的有( )个.
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,易证△ABP∽△PCD,从而得到BPPC=ABCD(不需证明)

探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,结论BPPC=ABCD仍成立吗?请说明理由?
拓展:如图③,在△ABC中,点P是BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=4 ![]() ,CE=3,则DE的长为 .
,CE=3,则DE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某手机店销售![]() 部
部![]() 型和
型和![]() 部
部![]() 型手机的利润为
型手机的利润为![]() 元,销售
元,销售![]() 部
部![]() 型和
型和![]() 部
部![]() 型手机的利润为
型手机的利润为![]() 元.
元.
(1)求每部![]() 型手机和
型手机和![]() 型手机的销售利润;
型手机的销售利润;
(2)该手机店计划一次购进![]() ,
,![]() 两种型号的手机共
两种型号的手机共![]() 部,其中
部,其中![]() 型手机的进货量不超过
型手机的进货量不超过![]() 型手机的
型手机的![]() 倍,设购进
倍,设购进![]() 型手机
型手机![]() 部,这
部,这![]() 部手机的销售总利润为
部手机的销售总利润为![]() 元.
元.
①求![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②该手机店购进![]() 型、
型、![]() 型手机各多少部,才能使销售总利润最大?
型手机各多少部,才能使销售总利润最大?
(3)在(2)的条件下,该手机店实际进货时,厂家对![]() 型手机出厂价下调
型手机出厂价下调![]() 元,且限定手机店最多购进
元,且限定手机店最多购进![]() 型手机
型手机![]() 部,若手机店保持同种手机的售价不变,设计出使这
部,若手机店保持同种手机的售价不变,设计出使这![]() 部手机销售总利润最大的进货方案.
部手机销售总利润最大的进货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下表所示,有A、B两组数:
第1个数 | 第2个数 | 第3个数 | 第4个数 | …… | 第9个数 | …… | 第n个数 | |
A组 | ﹣6 | ﹣5 | ﹣2 | …… | 58 | …… | n2﹣2n﹣5 | |
B组 | 1 | 4 | 7 | 10 | …… | 25 | …… |
(1)A组第4个数是 ;
(2)用含n的代数式表示B组第n个数是 ,并简述理由;
(3)在这两组数中,是否存在同一列上的两个数相等,请说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过点A(-1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线相应的函数表达式;
(2)点M是线段BC上的点(不与B、C重合),过M作MN∥y轴交抛物线于N,连接NB.若点M的横坐标为t,是否存在t,使MN的长最大?若存在,求出sin∠MBN的值;若不存在,请说明理由;
(3)若对一切x≥0均有ax2+bx+c≤mx-m+13成立,求实数m的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com