
| A. | 2.80m | B. | 2.816m | C. | 2.82m | D. | 2.826m |
分析 根据题意可以画出相应的抛物线,然后根据待定系数法求出抛物线的解析式,再根据题目中的数据即可求得该车要想通过此门,装货后的最大高度.
解答  解:如有右图所示,
解:如有右图所示,
设AB=4m,CH=4.4,EF=2.4,
设此抛物线的解析式为y=kx2,
则点A(-2,-4.4)在此抛物线上,
∴-4.4=k×(-2)2,
得k=-1.1,
∴y=-1.1x2,
∵点E的横坐标为-1.2,
则y=-1.1×(-1.2)2,得y=-1.584,
∴该车要想通过此门,装货后的最大高度应为:(-1.584)-(-4.4)=2.816m,
故选B.
点评 本题考查二次函数的应用,解答本题的关键是画出相应的抛物线,利用抛物线的性质和数形结合的思想解答.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
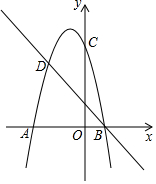 已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).
已知二次函数的图象与直线y=x+m交于x轴上一点A(-1,0),二次函数图象的顶点为C(1,-4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com