
【题目】如图,在△ABC中,∠C=90°,AC=BC,D为BC上一点,且DE⊥AB于E,若DE=CD,AB=8cm,则△DEB的周长为( )
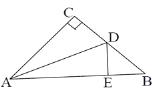
A.4cmB.8cmC.10cmD.14cm
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
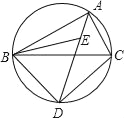
【题目】如图:△ABC是圆的内接三角形,∠BAC与∠ABC的角平分线AE、BE相交于点E,延长AE交圆于点D,连接BD、DC,且∠BCA=60°.
(1)求证:△BED为等边三角形;
(2)若∠ADC=30°,⊙O的半径为2![]() ,求BD长.
,求BD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知BC是⊙O的直径,点D是BC延长线上一点,AB=AD,AE是⊙O的弦,∠AEC=30°.
(1)求证:直线AD是⊙O的切线;
(2)若AE⊥BC,垂足为M,⊙O的半径为4,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种新型节能台灯共100盏,这两种台灯的进价、售价如表所示:
类型 价格 | 进价(元/盏) | 售价(元/盏) |
A型 | 25 | 45 |
B型 | 40 | 70 |
(1)若商场进货款为3100元,则这两种台灯各购进多少盏?
(2)若商场在3200元的限额内购进这两种台灯,且A型台灯的进货数量不超过B型台灯数量的3倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
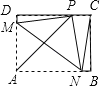
【题目】如图,在长方形纸片ABCD中,AB=12厘米,折叠纸片,使得点A落在CD边上的点P处,折痕为MN,点M、N分别在边AD、AB上,当点P恰好是CD边的中点时,点N与点B重合,若在折叠过程中NP=NC,则PD=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:把一张给定大小的矩形卡片ABCD放在宽度为10mm的横格纸中,恰好四个顶点都在横格线上,已知α=25°,求长方形卡片的周长。(精确到1mm,参考数据: sin25°≈0,cos25°≈0.9,tan25°≈0.5).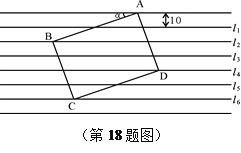
查看答案和解析>>
科目:初中数学 来源: 题型:
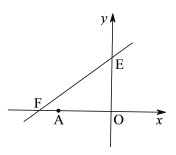
【题目】如图,直线![]() 与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线
与x轴、y轴分别相交于点F,E,点A的坐标为(-6,0),P(x,y)是直线![]() 上的一个动点.
上的一个动点.
(1)试写出点P在运动过程中,△OAP的面积S与x的函数关系式;
(2)当点P运动到什么位置,△OAP的面积为![]() ,求出此时点P的坐标.
,求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆客房部有60个房间供游客居住,当每个房间的定价为每天200元时,房间可以住满.当每个房间每天的定价每增加10元时,就会有一个房间空闲.对有游客入住的房间,宾馆需对每个房间每天支出20元的各种费用.
设每个房间每天的定价增加x元.求:
(1)房间每天的入住量y(间)关于x(元)的函数关系式;
(2)该宾馆每天的房间收费z(元)关于x(元)的函数关系式;
(3)该宾馆客房部每天的利润w(元)关于x(元)的函数关系式;当每个房间的定价为每天多少元时,w有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:如图1所示的图形,像我们常见的学习用品—圆规.我们不妨把这样图形叫做“规形图”.
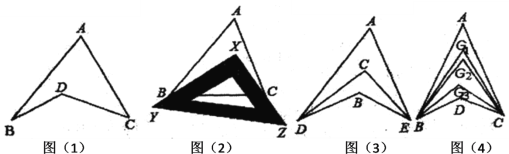
(1)观察“规形图”,试探究![]() 与
与![]() 、
、![]() 、
、![]() 之间的关系,并说明理由;
之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图2,把一块三角尺![]() 放置在
放置在![]() 上,使三角尺的两条直角边
上,使三角尺的两条直角边![]() 、
、![]() 恰好经过点
恰好经过点![]() 、
、![]() ,
,![]() ,则
,则![]() ________________;
________________;
②如图3,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
③如图4,![]() ,
,![]() 的
的![]() 等分线相交于点
等分线相交于点![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com