
【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20 ![]() 米.
米.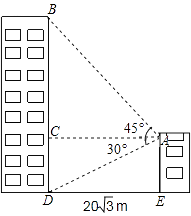
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
【答案】
(1)
解:如图,∵AC⊥BD,
∴BD⊥DE,AE⊥DE,
∴四边形AEDC是矩形,
∴AC=DE=20 ![]() 米,
米,
∵在Rt△ABC中,∠BAC=45°,
∴BC=AC=20 ![]() 米,
米,
在Rt△ACD中,tan30°= ![]() ,
,
∴CD=ACtan30°=20 ![]() ×
× ![]() =20(米),
=20(米),
∴BD=BC+CD=20 ![]() +20(米);
+20(米);
∴大厦的高度BD为:(20 ![]() +20)米
+20)米
(2)
解:∵四边形AEDC是矩形,
∴AE=CD=20米.
∴小敏家的高度AE为20米
【解析】(1)易得四边形AEDC是矩形,即可求得AC的长,然后分别在Rt△ABC与Rt△ACD中,利用三角函数的知识求得BC与CD的长,继而求得答案;(2)结合(1),由四边形AEDC是矩形,即可求得小敏家的高度AE.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中(如图每格一个单位),描出下列各点A(﹣2,﹣1),B(2,﹣1),C(2,2),D(3,2),E(0,3),F(﹣3,2),G(﹣2,2),A(﹣2,﹣1)并依次将各点连接起来,观察所描出的图形,它像什么?根据图形回答下列问题:
(1)图形中哪些点在坐标轴上,它们的坐标有什么特点?
(2)线段FD和x轴有什么位置关系?点F和点D的坐标有什么特点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ![]() ,1)在反比例函数y=
,1)在反比例函数y= ![]() 的图象上.
的图象上.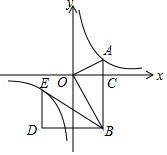
(1)求k的值;
(2)若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
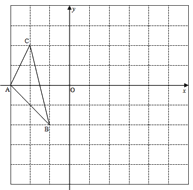
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:A(-3,0),B(-1,-2),C(-2,2).
(1)请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.
(2)请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条不完整的数轴上从左到右有点A,B,C,其中AB=2,BC=1,如图所示.设点A,B,C所对应数的和是p.

(1)若以B为原点,写出点A,C所对应的数,并计算p的值;若以C为原点,p又是多少?
(2)若原点O在图中数轴上点C的右边,且CO=28,求p.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是△ABC中BC边上的一点,且BE= ![]() BC;点D是AC上一点,且AD=
BC;点D是AC上一点,且AD= ![]() AC,S△ABC=24,则S△BEF﹣S△ADF=( )
AC,S△ABC=24,则S△BEF﹣S△ADF=( ) 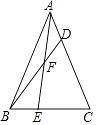
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为:x+3=2,解得x=﹣1
当x+3<0时,原方程可化为:x+3=﹣2,解得x=﹣5
所以原方程的解是x=﹣1,x=﹣5
(1)解方程:|3x﹣2|﹣4=0;
(2)探究:当b为何值时,方程|x﹣2|=b ①无解;②只有一个解;③有两个解.
(3)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题6分)某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下:
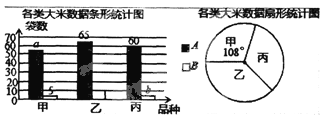
根据所给信息,解决下列问题:
(1)a=_______,b=_______.
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?请简述理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com