
【题目】如图,E是△ABC中BC边上的一点,且BE= ![]() BC;点D是AC上一点,且AD=
BC;点D是AC上一点,且AD= ![]() AC,S△ABC=24,则S△BEF﹣S△ADF=( )
AC,S△ABC=24,则S△BEF﹣S△ADF=( ) 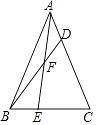
A.1
B.2
C.3
D.4
【答案】B
【解析】解:过D作DG∥AE交CE于G, ∵AD= ![]() AC,
AC,
∴CG=3EG,
∴AE= ![]() DG,CE=
DG,CE= ![]() CG,
CG,
∵EC=2BE,
∴BE=2EG,
∴EF= ![]() DG,
DG,
∴AF= ![]() DG,
DG,
∴EF=AF,
∵S△ABC=24,
∴S△ABD= ![]() S△ABC=6.
S△ABC=6.
∵EC=2BE,S△ABC=24,
∴S△ABE= ![]() S△ABC=8,
S△ABC=8,
∵S△ABE﹣S△ABD=(S△ABF+S△BEF)﹣(S△ADF+S△ABF)=S△BEF﹣S△ADF ,
即S△BEF﹣S△ADF=S△ABE﹣S△ABD=8﹣6=2.
故选B.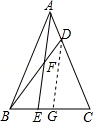
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高.


科目:初中数学 来源: 题型:
【题目】“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73)
≈1.73) 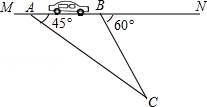
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的面积为6,AC=3,现将△ABC沿AB所在直线翻折,使点C落在直线AD上的C′处,P为直线AD上的一点,则线段BP的长不可能是( ) 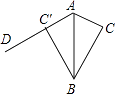
A.3
B.4
C.5.5
D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小敏家对面新建了一幢图书大厦,小敏在自家窗口测得大厦顶部的仰角为45°,大厦底部的仰角为30°,如图所示,量得两幢楼之间的距离为20 ![]() 米.
米.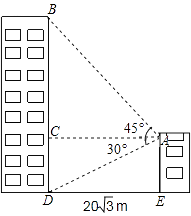
(1)求出大厦的高度BD;
(2)求出小敏家的高度AE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( ) 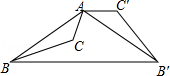
A.55°
B.65°
C.75°
D.85°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在如图所示的数轴上,把数﹣2, ![]() ,4,﹣
,4,﹣![]() ,2.5表示出来,并用“<“将它们连接起来;
,2.5表示出来,并用“<“将它们连接起来;
(2)假如在原点处放立一挡板(厚度不计),有甲、乙两个小球(忽略球的大小,可看作一点),小球甲从表示数﹣2的点处出发,以1个单位长度/秒的速度沿数轴向左运动;同时小球乙从表示数4的点处出发,以2个单位长度/秒的速度沿数轴向左运动,在碰到挡板后即刻按原来的速度向相反的方向运动,设运动的时间为t(秒).
请从A,B两题中任选一题作答.
A.当t=3时,求甲、乙两小球之间的距离.
B.用含t的代数式表示甲、乙两小球之间的距离.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小赵和小王交流暑假中的活动,小赵说:“我们一家外出旅行了一个星期,这7天的日期数之和是84天,你知道我们几号出去的么?”小王说“我暑假去舅舅家住了7天,日历数再加月份数也是84,你能猜出我是几月几号回的家?试试看列出方程,解决小赵、小王的问题.(提示:7月1日﹣9月1日暑假) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形周长为8![]() ,底边BC长为
,底边BC长为![]() ,腰AB长为
,腰AB长为![]() ,
,
(1)写出![]() 关于
关于![]() 的函数关系式__________________;
的函数关系式__________________;
(2)写出![]() 的取值范围_____________;写出
的取值范围_____________;写出![]() 的取值范围_____________.
的取值范围_____________.
(3)画出这个函数的图象.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xoy中,点A、B的坐标分别是A(-1,0),B(3,0),将线段AB向上平移2个单位,再向右平移1个单位,得到线段DC,点A、B的对应点分别是D、C,连接AD、BC.
(1)直接写出点C,D的坐标;
(2)求四边形ABCD的面积;
(3)点P为线段BC上任意一点(与点B、C不重合),连接PD,PO.求证:∠CDP+∠BOP=∠OPD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com