
【题目】(1)在如图所示的数轴上,把数﹣2, ![]() ,4,﹣
,4,﹣![]() ,2.5表示出来,并用“<“将它们连接起来;
,2.5表示出来,并用“<“将它们连接起来;
(2)假如在原点处放立一挡板(厚度不计),有甲、乙两个小球(忽略球的大小,可看作一点),小球甲从表示数﹣2的点处出发,以1个单位长度/秒的速度沿数轴向左运动;同时小球乙从表示数4的点处出发,以2个单位长度/秒的速度沿数轴向左运动,在碰到挡板后即刻按原来的速度向相反的方向运动,设运动的时间为t(秒).
请从A,B两题中任选一题作答.
A.当t=3时,求甲、乙两小球之间的距离.
B.用含t的代数式表示甲、乙两小球之间的距离.
![]()
【答案】(1)答案见解析(2)A.7;B.0<t≤2时,6-t;t>2时,3t-2.
【解析】试题分析:(1)先将各数表示在数轴上,然后按照数轴上越右的数越大用“<”号连接起来即可;
(2)甲球到原点的距离=甲球运动的路程+OA的长,乙球到原点的距离分两种情况:(Ⅰ)当0<t≤2时,乙球从点B处开始向左运动,一直到原点O,此时OB的长度-乙球运动的路程即为乙球到原点的距离;(Ⅱ)当t>2时,乙球从原点O处开始向右运动,此时乙球运动的路程-OB的长度即为乙球到原点的距离;
A、当t=3时,根据上面的分析进行计算即可得;
B、分0<t≤2与t>2两种情况进行讨论即可得.
试题解析:(1)如图所示:
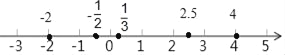
-2<-![]() <
<![]() <2.5<4;
<2.5<4;
(2)∵甲球运动的路程为:1t=t,OA=2,∴甲球与原点的距离为:t+2;
乙球到原点的距离分两种情况:
(Ⅰ)当0<t≤2时,乙球从点B处开始向左运动,一直到原点O,
∵OB=4,乙球运动的路程为:2t=2t,∴乙球到原点的距离为:4-2t;
(Ⅱ)当t>2时,乙球从原点O处开始一直向右运动,此时乙球到原点的距离为:2(t-2)=2t-4;
A、当t=3时,甲、乙两小球之间的距离为:t+2+2t-4=3t-2=7;
B、分两种情况:(Ⅰ)0<t≤2,甲、乙两小球之间的距离为:t+2+4-2t=6-t;
(Ⅱ)t>2,甲、乙两小球之间的距离为:t+2+2t-4=3t-2.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.
(1)设A,B两种商品每件售价分别为a元、b元,求a、b的值;
(2)B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件. ①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
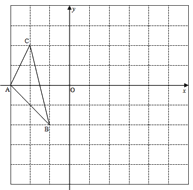
【题目】如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标分别为:A(-3,0),B(-1,-2),C(-2,2).
(1)请在图中画出△ABC绕B点顺时针旋转90°后的图形△A′BC′.
(2)请直接写出以A′、B、C′为顶点平行四边形的第4个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是△ABC中BC边上的一点,且BE= ![]() BC;点D是AC上一点,且AD=
BC;点D是AC上一点,且AD= ![]() AC,S△ABC=24,则S△BEF﹣S△ADF=( )
AC,S△ABC=24,则S△BEF﹣S△ADF=( ) 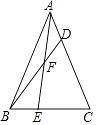
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列解题过程,然后解答问题
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为:x+3=2,解得x=﹣1
当x+3<0时,原方程可化为:x+3=﹣2,解得x=﹣5
所以原方程的解是x=﹣1,x=﹣5
(1)解方程:|3x﹣2|﹣4=0;
(2)探究:当b为何值时,方程|x﹣2|=b ①无解;②只有一个解;③有两个解.
(3)![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
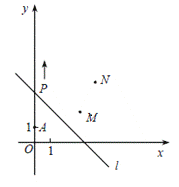
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿![]() 轴以每秒1个单位长的速度向上移动,且过点P的直线
轴以每秒1个单位长的速度向上移动,且过点P的直线![]() 也随之移动,设移动时间为
也随之移动,设移动时间为![]() 秒.
秒.
(1)当![]() 时,求直线的解析式;
时,求直线的解析式;
(2)若点M,N位于直线的异侧,确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A、B两点,与y轴交C点,点A的坐标为(2,0),点C的坐标为(0,3)它的对称轴是直线x= ![]() .
.
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com