
【题目】在数轴上点A表示-3,点B表示4.
(1)点A与点B之间的距离是 ;
(2)我们知道,在数轴上|a|表示数a所对应的点到原点的距离,你能说明![]() 在数轴上表示的意义吗?
在数轴上表示的意义吗?
(3)在数轴上点P表示的数为x,是否存在这样的点P,使2PA+PB=12?若存在,请求出相应的x;若不存在,请说明理由.
![]()
【答案】(1)7;(2)见解析;(3)存在,x=![]() 或2
或2
【解析】
(1)根据数轴上两点距离公式计算即可.
(2)根据绝对值的几何意义即可得出
(3)根据数轴上两点距离公式,分三类讨论:①当P在点A左侧时;②当点P在AB之间时;③当P在B右侧时.
解:(1)4-(-3)=7
∴点A与点B之间的距离是7
故答案为:7
(2)∵在数轴上|a|表示数a所对应的点到原点的距离,
∴在数轴上![]() 表示数-3的点和数-5的点之间的距离
表示数-3的点和数-5的点之间的距离
(3)①当P在点A左侧时,PA=-3-x,PB=4-x;
∵2PA+PB=12
∴2(-3-x)+(4-x) =12
∴x=![]()
②当点P在AB之间时;PA=x+3,PB=4-x;
∴2(x+3)+(4-x) =12
∴x=2
③当P在B右侧时;PA=x+3,PB=x-4;
∴2(x+3)+(x-4) =12
∴x=![]() 不合题意舍去
不合题意舍去
综上所述:当x=![]() 或2时,使2PA+PB=12
或2时,使2PA+PB=12


科目:初中数学 来源: 题型:
【题目】将若干个同样大小的小长方形纸片拼成如图形状的大长方形![]() 小长方形纸片长为a,宽为
小长方形纸片长为a,宽为![]() ,请你仔细观察图形,解答下列问题:
,请你仔细观察图形,解答下列问题:
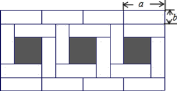
(1)a和b之间的关系满足_____________________.
(2)图中阴影部分的面积与大长方形面积的比值是___________.
(3)请你仔细观察图中的一个阴影部分,根据它面积的不同表示方法,请你写出![]() ,
,![]() 与
与![]() 三个代数式之间的等量关系_________________________
三个代数式之间的等量关系_________________________
应用:根据探索中的等量关系,解决如下问题:![]() 求
求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民生活用水的费用由“城市供水费” 和“污水处理费”两部分组成.为了鼓励市民节约用水, 其中城市供水费按阶梯式计费:一个月用水 10 吨以内(包括 10 吨)的用户,每吨收 1.5 元;一个月用水超过 10 吨的用户,10 吨水仍按每吨 1.5 元收费,超过 10 吨的部分,按每吨 2 元收费.另外污水处理费按每吨 0.65 元收取.
(1)某居民 5 月份用水 8 吨,应交水费多少元?
(2)某居民 6 月份用水 12 吨,应交水费多少元?
(3)若某户某月用水 x 吨,请你用含有 x 的代数式表示该月应交的水费
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一个平面去截正方体(如图),下列关于截面(截出的面)形状的结论:
①可能是锐角三角形;②可能是钝角三角形;
③可能是长方形;④可能是梯形.
其中正确结论的是______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读思考:
数学课上老师出了一道分式化简求值题目.
题目:![]() ÷(x+1)·
÷(x+1)·![]() -
-![]() ,其中x=-
,其中x=-![]() .
.
“勤奋”小组的杨明同学展示了他的解法:
解:原式=![]() -
-![]() ..................第一步
..................第一步
=![]() -
-![]() ................ ..第二步
................ ..第二步
=![]() ..........................第三步
..........................第三步
=![]() ..................................第四步
..................................第四步
当x=-![]() 时,原式=
时,原式= .......................第五步
.......................第五步
请你认真阅读上述解题过程,并回答问题:
你认为该同学的解法正确吗?如有错误,请指出错误在第几步,并写出完整、正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示是一枚质地均匀的骰子.骰子有六个面并分别代表数字1,2,3,4,5,6.如图2,正六边形ABCDEF的顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子向上的一面上的点数是几,就沿正六边形的边顺时针方向连续跳几个边长.如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从圈D开始顺时针连续跳2个边长,落到圈F……
设游戏者从圈A起跳.
(1)小明随机掷一次骰子,求落回到圈A的概率P1;
(2)小亮随机掷两次骰子,用列表法或画树状图法求最后落回到圈A的概率P2,并指出他与小明落回到圈A的可能性一样吗?
 图1
图1 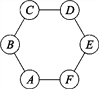 图2
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
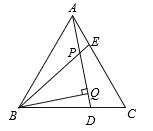
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象关于
的图象关于![]() 轴对称,
轴对称,![]() ,
,![]() 是函数
是函数![]() 图象上的两点,连接
图象上的两点,连接![]() ,点
,点![]() 是函数
是函数![]() 图象上的一点,连接
图象上的一点,连接![]() ,
,![]() .
.
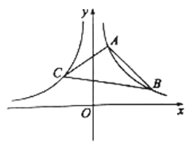
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 所在直线的表达式;
所在直线的表达式;
(3)求![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com