
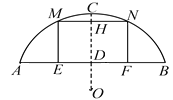
【题目】如图,某地有一座圆弧形的拱桥,桥下水面宽为7.2m,拱顶高出水面2.4m,现有一艘宽3m,船舱顶部为正方形并高出水面2m的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
【答案】货船能顺利通过这座拱桥,理由见解析.
【解析】试题分析:根据题意画出图形,利用垂径定理和勾股定理求出拱桥的半径长,连接ON,OA,通过求距离水面2米高处即HD长为2时,桥有多宽即MN的长与货船顶部的3米做比较来判定货船能否通过(MN大于3则能通过,MN小于等于3则不能通过).先根据半弦,半径和弦心距构造直角三角形求出半径的长,再根据Rt△OHN中勾股定理求出HN的长,从而求得MN的长.
试题解析:如图,连接ON,OA,
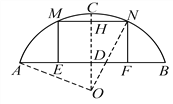
∵OC⊥AB,
∴D为AB中点,
∵AB=7.2m,
∴AD=![]() AB=3.6m.
AB=3.6m.
又∵CD=2.4m,
设OA=OC=ON=r,则OD=(r-2.4)m,
在Rt△AOD中,根据勾股定理得:r2=(r-2.4)2+3.62,解得r=3.9,
∵CD=2.4m,船舱顶部为正方形并高出水面AB=2m,
∴CH=2.4-2=0.4(m),
∴OH=r-CH=3.9-0.4=3.5(m),
在Rt△OHN中,HN2=ON2-OH2=3.92-3.52=2.96(m2),
∴HN=![]() (m),
(m),
∴MN=2EN=2×![]() ≈3.44m>3m,
≈3.44m>3m,
∴此货船能顺利通过这座拱桥.


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案科目:初中数学 来源: 题型:
【题目】某班要购买一批篮球和足球.已知篮球的单价比足球的单价贵40元,花1500元购买的篮球的个数与花900元购买的足球的个数恰好相等.
(1)篮球和足球的单价各是多少元?
(2)若该班恰好用完1000元购买的篮球和足球,则购买的方案有哪几种?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】骑共享单车已成为人们喜爱的一种绿色出行方式.已知A、B、C三家公司的共享单车都是按骑车时间收费,标准如下:
公司 | 单价(元/半小时) | 充值优惠 |
A | m | 充20元送5元,即:充20元实得25元 |
B | m-0.2 | 无 |
C | 1 | 充20元送20元,即:充20元实得40元 |
(注:使用这三家公司的共享单车,不足半小时均按半小时计费.用户的账户余额长期有效,但不可提现.)
4月初,李明注册成了A公司的用户,张红注册成了B公司的用户,并且两人在各自账户上分别充值20元.一个月下来,李明、张红两人使用单车的次数恰好相同,且每次都在半小时以内,结果到月底李明、张红的账户余额分别显示为5元、8元.
(1)求m的值;
(2)5月份,C公司在原标准的基础上又推出新优惠:每月的月初给用户送出5张免费使用券(1
次用车只能使用1张券).如果王磊每月使用单车的次数相同,且在30次以内,每次用车都不超过
半小时. 若要在这三家公司中选择一家并充值20元,仅从资费角度考虑,请你帮他作出选择,并说
明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.有两条边对应相等的两个三角形全等
B.两腰对应相等的两个等腰三角形全等
C.两角对应相等的两个等腰三角形全等
D.一边对应相等的两个等边三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣7)﹣(+5)+(﹣4)﹣(﹣10);
(2)![]() .
.
(3)(﹣24)×(1+![]() ﹣
﹣![]() );
);
(4)36÷(﹣3)2×(![]() ﹣1)+(﹣1)3+(﹣1)2.
﹣1)+(﹣1)3+(﹣1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,对角线AC与BD相交于点O,不能判断四边形ABCD是平行四边形的是( )

A.AB=DC,AD=BCB.AB∥DC,AD∥BC
C.AB∥DC,AD=BCD.OA=OC,OB=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D是∠AOB的平分线OC上任意一点,过D作DE⊥OB于E,以DE为半径作⊙D,
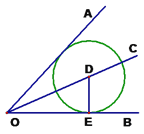
①判断⊙D与OA的位置关系, 并证明你的结论。
②通过上述证明,你还能得出哪些等量关系?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com