
���� ��1����A��B����Ʒ�ƵĻ�ױƷÿ���۷ֱ�Ϊ����Ԫ������A��Ʒ�ƵĻ�ױƷÿ����ΪxԪ��B��Ʒ�ƵĻ�ױƷÿ����ΪyԪ���������ֹ������г���������⼴�ɣ�
��2�����蹺����AƷ�ƻ�ױƷx�ף����ݹ���BƷ�ƻ�ױƷ�������ȹ���AƷ�ƻ�ױƷ������2������4�ף����ɵó��𰸣�
������A��Ʒ�Ƶû�ױƷ����m�ף�����ʹ�ܵĻ���������1200Ԫ���ٸ���BƷ�ƻ�ױƷ���ɹ���40�ף��г�����ʽ�飬��⼴�ɣ�
��� �⣺��1����A��Ʒ�ƵĻ�ױƷÿ����ΪxԪ��B��Ʒ�ƵĻ�ױƷÿ����ΪyԪ��
��$\left\{\begin{array}{l}{5x+6y=950}\\{3x+2y=450}\end{array}\right.$��
���$\left\{\begin{array}{l}{x=100}\\{y=75}\end{array}\right.$��
��A��B����Ʒ�Ƶû�ױƷÿ���۷ֱ�Ϊ100Ԫ��75Ԫ��
��2�����蹺����AƷ�ƻ�ױƷx�ף��ú�x�Ĵ���ʽ��ʾ������BƷ�ƻ�ױƷ������Ϊ��2x+4���ף�
�ʴ�Ϊ��2x+4��
����A��Ʒ�Ƶû�ױƷ����m�ף���B��Ʒ�Ƶû�ױƷ������2m+4���ף�
��������ã�$\left\{\begin{array}{l}{2m+4��40}\\{30m+20��2m+4����1200}\end{array}\right.$��
���16��m��18��
��m��������
��m=16��17��18��
��2m+4=36��38��40��
�������ֽ���������
��һ�ַ�����A��Ʒ�Ƶû�ױƷ����16�ף�B��Ʒ�Ƶû�ױƷ����36�ף�
�ڶ��ַ�����A��Ʒ�Ƶû�ױƷ����17�ף�B��Ʒ�Ƶû�ױƷ����38�ף�
�����ַ�����A��Ʒ�Ƶû�ױƷ����18�ף�B��Ʒ�Ƶû�ױƷ����40�ף�
���� ���⿼����һԪһ�β���ʽ��Ͷ�Ԫһ�η������Ӧ�ã���Ӧ����Ĺؼ��Ƕ������⣬�ҵ��ؼ�����������ҵ���������ĵ�����ϵ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
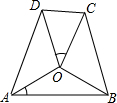 ��ͼ��OΪ�ı���ABCD��һ�㣬OA=OB=OC=OD����AOB���CDO��������OAB���COD��ȣ���$\frac{AB}{CD}$==$\frac{3+\sqrt{5}}{2}$��
��ͼ��OΪ�ı���ABCD��һ�㣬OA=OB=OC=OD����AOB���CDO��������OAB���COD��ȣ���$\frac{AB}{CD}$==$\frac{3+\sqrt{5}}{2}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1��2��3 | B�� | 1��5��5 | C�� | 3��3��6 | D�� | 3��5��1 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com