
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬AC=4��BC=3��P������AB�ϵ�һ�����㣬�Ե�PΪԲ�ģ�PAΪ�뾶�ġ�P������AC����һ������ΪD��ֱ��PD��ֱ��BC�ڵ�E��
��1������D��AC���е㣬���P�İ뾶AP�ij���
��2����AP=2����CE�ij���
��3�����߶�BE���е�ΪQ������PQ���P�ཻ�ڵ�I����P���˶��Ĺ����У�����D��C�� I��P����һ��ƽ���ı���ʱ����ֱ��д������AP�ij���
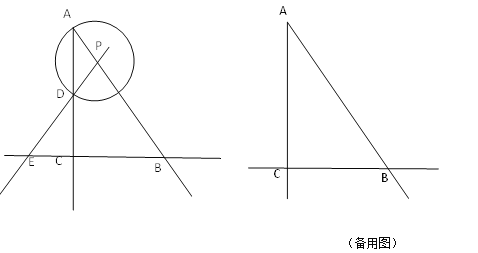
���𰸡���1��AP=![]() ����2��CE=
����2��CE=![]() ����3��AP=
����3��AP=![]() ��AP=
��AP=![]()
�������������������1������P��PF��y���ڵ�F����������Ǻ����Ķ���ó�tan��PAF=![]() =
=![]() =
=![]() ���ٸ��ݴ��������ó�AF�ij������ݹ��ɶ������ɵó����ۣ���2�������������ε��ж������ó���ABC�ס�DEC����Rt��ABC�У����ݹ��ɶ������AB�ij����ٸ���������Ǻ����Ķ��弴�ɵó����ۣ���3�����ݵ�P���߶�AB�ϣ���E���߶�BC�ӳ����ϣ���P���߶�AB�ϣ���E���߶�BC�ϣ���P���߶�AB���ӳ���������������з������ۣ�
���ٸ��ݴ��������ó�AF�ij������ݹ��ɶ������ɵó����ۣ���2�������������ε��ж������ó���ABC�ס�DEC����Rt��ABC�У����ݹ��ɶ������AB�ij����ٸ���������Ǻ����Ķ��弴�ɵó����ۣ���3�����ݵ�P���߶�AB�ϣ���E���߶�BC�ӳ����ϣ���P���߶�AB�ϣ���E���߶�BC�ϣ���P���߶�AB���ӳ���������������з������ۣ�
�����������1������P��PF��y���ڵ�F��

����Rt��ABC��,��ACB=90�㣬AC=4��BC=3��
��tan��PAF=![]() =
=![]() =
=![]() ��
��
�ߵ�D��AC���е㣬
��AD=2��
��AF=1��
��![]() =
=![]() ,���PF=
,���PF=![]() ��
��
��AP=![]() =
=![]() =
=![]() .
.
(2)��AP=DP��
���PAD=��PDA��
�ߡ�PDA=��CDE��
���PAD=��CDE��
�ߡ�ACB=��DCE=90�㣬
���ABC�ס�DEC��
���ABC=��DEC��![]() ��
��
��PB=PE��
Rt��ABC�У���ABC=90�㣬AC=4��BC=3��
��AB=5��
��AP=2��
��PB=PE=3��DE=1
��![]() ��CE=
��CE=![]() ��
��
��3��AP=![]() ��AP=
��AP=![]() ��
��
��AP=x��
�������P���߶�AB�ϣ���E���߶�BC�ӳ�����ʱ����ͼ2����
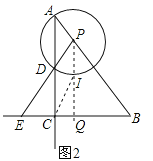
�ɣ�2��֪����ABC�ס�DEC��
��![]()
��![]() ��DC=
��DC=![]() ��5-2x��,
��5-2x��,
��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ���DC=PI�ã�![]() ��5-2x��= x��x=
��5-2x��= x��x=![]() ��
��
�������P���߶�AB�ϣ���E���߶�BC��ʱ����ͼ3����
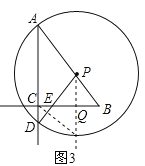
DC=![]() ��2x -5��, ��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ�
��2x -5��, ��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ�
��DC=PI�ã�![]() ��2x -5��= x��x=
��2x -5��= x��x=![]() ��
��
��![]() ��5�����P���߶�AB��ì�ܣ���x=
��5�����P���߶�AB��ì�ܣ���x=![]() ��ȥ��
��ȥ��
�������P���߶�AB���ӳ����ϣ���ͼ4����

��E���߶�BC���ӳ�����ʱ�� DC=![]() ��2x -5��, ��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ���DC=PI�ã�
��2x -5��, ��DC=PIʱ����D��C�� I��P����һ��ƽ���ı��Σ���DC=PI�ã�![]() ��2x -5��= x��x=
��2x -5��= x��x=![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ͬѧ���в������ŷֱ��������![]() ��
��![]() ��1�Ŀ�Ƭ����ͬѧ���в������ŷֱ��������1��3��2�Ŀ�Ƭ����Ƭ������ͬ���ִӼ����������и���ȡһ�ſ�Ƭ���������ǵ����ֱַ��Ϊa��b��
��1�Ŀ�Ƭ����ͬѧ���в������ŷֱ��������1��3��2�Ŀ�Ƭ����Ƭ������ͬ���ִӼ����������и���ȡһ�ſ�Ƭ���������ǵ����ֱַ��Ϊa��b��
��1������������ͼ���б����г����п��ܵĽ����
��2�����ƶ�һ����Ϸ��������ѡ����a��b��ʹ��ax2+bx+1=0����������ȵ�ʵ���������ʤ�������һ�ʤ��������������Ϸ����ƽ�����ø���֪ʶ���ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�������Ŀڴ��У�װ�����ɸ������4���������dz���ɫ��û���κ�����ҡ�Ⱥ�����������һ��������ɫ���ٷŻؿڴ��У�ͨ�������ظ�����ʵ�鷢�֣����������Ƶ����0.2������ƺ����д�Լ�к�������
A.16��
B.20��
C.25��
D.30��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ����,��ʦ����һ����:����
[8(a+b)5-4(a+b)4+(-a-b)3]��[2(a+b)3].
С��ͬѧ���Ͼ���,������С���Ľ������:
[8(a+b)5-4(a+b)4+(-a-b)3]��[2(a+b)3]
=[8(a+b)5-4(a+b)4+(a+b)3]��8(a+b)3
=(a+b)2-![]() (a+b)+
(a+b)+ ![]() .
.
С��Ҳ��������,˵С���Ľ�����̲���,��ָ�˳���.��ʦ�϶���С���Ļش�.��֪��С�������Ķ���?��ָ����,��д����ȷ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��һ�·�����ij����100̨���ƻ����·�����144̨����������·�ÿ�µ�ƽ��������Ϊx�����������г��ķ����ǣ�������
A.100��1+x��2��144B.100��1��x��2��144
C.144��1+x��2��100D.144��1��x��2��100
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������x��һԪ���η��̣�k��1��x2��2x+1=0����������ȵ�ʵ��������ʵ��k��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ʽ(a��1)x>a��1�Ľ⼯��x<1����ôa��ȡֵ��Χ��(����)
A. a��1B. a<1C. a��1D. a<0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
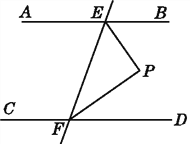
����Ŀ����ͼ,��֪AB��CD,ֱ��EF�ֱ�AB,CD�ڵ�E,F,EPƽ����BEF,FPƽ����DFE.��˵��:��PEF��ֱ��������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com