
【题目】某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).
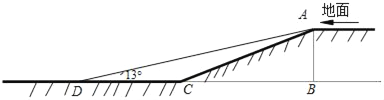
(1)求这个车库的高度AB;
(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).
(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)
【答案】(1)这个车库的高度AB为5米;(2)斜坡改进后的起点D与原起点C的距离为9.7米.
【解析】
(1)根据坡比可得![]() =
=![]() ,利用勾股定理求出AB的长即可;(2)由(1)可得BC的长,由∠ADB的余切值可求出BD的长,进而求出CD的长即可.
,利用勾股定理求出AB的长即可;(2)由(1)可得BC的长,由∠ADB的余切值可求出BD的长,进而求出CD的长即可.
(1)由题意,得:∠ABC=90°,i=1:2.4,
在Rt△ABC中,i=![]() =
=![]() ,
,
设AB=5x,则BC=12x,
∴AB2+BC2=AC2,
∴AC=13x,
∵AC=13,
∴x=1,
∴AB=5,
答:这个车库的高度AB为5米;
(2)由(1)得:BC=12,
在Rt△ABD中,cot∠ADC=![]() ,
,
∵∠ADC=13°,AB=5,
∴DB=5cot13°≈21.655(m),
∴DC=DB﹣BC=21.655﹣12=9.655≈9.7(米),
答:斜坡改进后的起点D与原起点C的距离为9.7米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC∽△A′B′C′,AB=4 cm,A′B′=3 cm,AD,A′D′分别为△ABC与△A′B′C′的中线,下列结论中:①AD∶A′D′=4∶3;②△ABD∽△A′B′D′;③△ABD∽△A′B′C′;④△ABC与△A′B′C′对应边上的高之比为4∶3.其中结论正确的序号是_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
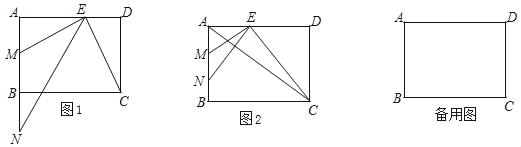
(1)如图1,求证:∠ANE=∠DCE;
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2﹣2ax﹣3(a≠0)的图象经过点A.
(1)求二次函数的对称轴;
(2)当A(﹣1,0)时,
①求此时二次函数的表达式;
②把y=ax2﹣2ax﹣3化为y=a(x﹣h)2+k的形式,并写出顶点坐标;
③画出函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
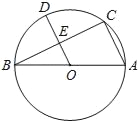
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E.
(1)求证:OD∥AC;
(2)若BC=8,DE=3,求⊙O的直径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com