
【题目】在矩形ABCD中,AB=6,AD=8,点E是边AD上一点,EM⊥BC交AB于点M,点N在射线MB上,且AE是AM和AN的比例中项.
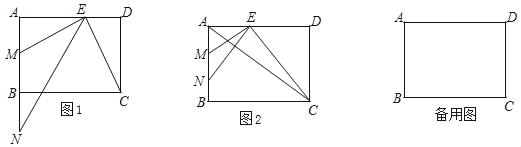
(1)如图1,求证:∠ANE=∠DCE;
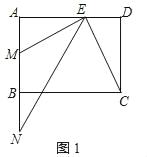
(2)如图2,当点N在线段MB之间,联结AC,且AC与NE互相垂直,求MN的长;
(3)连接AC,如果△AEC与以点E、M、N为顶点所组成的三角形相似,求DE的长.
【答案】(1)见解析;(2)![]() ;(3)DE的长分别为
;(3)DE的长分别为![]() 或3.
或3.
【解析】
(1)由比例中项知![]() ,据此可证△AME∽△AEN得∠AEM=∠ANE,再证∠AEM=∠DCE可得答案;
,据此可证△AME∽△AEN得∠AEM=∠ANE,再证∠AEM=∠DCE可得答案;
(2)先证∠ANE=∠EAC,结合∠ANE=∠DCE得∠DCE=∠EAC,从而知![]() ,据此求得AE=8﹣
,据此求得AE=8﹣![]() =
=![]() ,由(1)得∠AEM=∠DCE,据此知
,由(1)得∠AEM=∠DCE,据此知![]() ,求得AM=
,求得AM=![]() ,由求得
,由求得![]() MN=
MN=![]() ;
;
(3)分∠ENM=∠EAC和∠ENM=∠ECA两种情况分别求解可得.
解:(1)∵AE是AM和AN的比例中项
∴![]() ,
,
∵∠A=∠A,
∴△AME∽△AEN,
∴∠AEM=∠ANE,
∵∠D=90°,
∴∠DCE+∠DEC=90°,
∵EM⊥BC,
∴∠AEM+∠DEC=90°,
∴∠AEM=∠DCE,
∴∠ANE=∠DCE;
(2)∵AC与NE互相垂直,
∴∠EAC+∠AEN=90°,
∵∠BAC=90°,
∴∠ANE+∠AEN=90°,
∴∠ANE=∠EAC,
由(1)得∠ANE=∠DCE,
∴∠DCE=∠EAC,
∴tan∠DCE=tan∠DAC,
∴![]() ,
,
∵DC=AB=6,AD=8,
∴DE=![]() ,
,
∴AE=8﹣![]() =
=![]() ,
,
由(1)得∠AEM=∠DCE,
∴tan∠AEM=tan∠DCE,
∴![]() ,
,
∴AM=![]() ,
,
∵![]() ,
,
∴AN=![]() ,
,
∴MN=![]() ;
;
(3)∵∠NME=∠MAE+∠AEM,∠AEC=∠D+∠DCE,
又∠MAE=∠D=90°,由(1)得∠AEM=∠DCE,
∴∠AEC=∠NME,
当△AEC与以点E、M、N为顶点所组成的三角形相似时
①∠ENM=∠EAC,如图2,
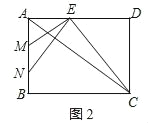
∴∠ANE=∠EAC,
由(2)得:DE=![]() ;
;
②∠ENM=∠ECA,
如图3,
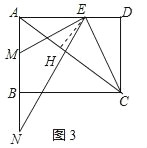
过点E作EH⊥AC,垂足为点H,
由(1)得∠ANE=∠DCE,
∴∠ECA=∠DCE,
∴HE=DE,
又tan∠HAE=![]() ,
,
设DE=3x,则HE=3x,AH=4x,AE=5x,
又AE+DE=AD,
∴5x+3x=8,
解得x=1,
∴DE=3x=3,
综上所述,DE的长分别为![]() 或3.
或3.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】对于钝角α,定义它的三角函数值如下:sinα=sin (180°-α),cosα=-cos (180°-α);若一个三角形的三个内角的比是1∶1∶4,A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,点F在线段DE上,过点F作FG∥AB、FH∥AC分别交BC于点G、H,如果BG:GH:HC=2:4:3.求![]() 的值.
的值.
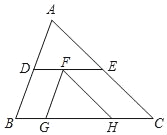
查看答案和解析>>
科目:初中数学 来源: 题型:
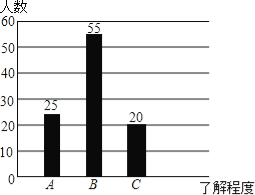
【题目】阳光中学组织学生开展社会实践活动,调查某社区居民对消防知识的了解程度(A:特别熟悉,B:有所了解,C:不知道),在该社区随机抽取了100名居民进行问卷调查,将调查结果制成如图所示的统计图,根据统计图解答下列问题:
(1)若该社区有居民900人,试估计对消防知识“特别熟悉”的居民人数;
(2)该社区的管理人员有男、女个2名,若从中选2名参加消防知识培训,试用列表或画树状图的方法,求恰好选中一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).
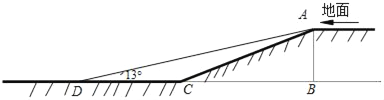
(1)求这个车库的高度AB;
(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).
(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】环保局对某企业排污情况进行检测,结果显示,所排污水中硫化物的浓度超标,即硫化物的浓度超过最高允许的![]() ,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度
,环保局要求该企业立即整改,在15天以内(含15天)排污达标,整改过程中,所排污水中硫化物的浓度![]() 与时间
与时间![]() (天)的变化规律如图所示,其中线段
(天)的变化规律如图所示,其中线段![]() 表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度
表示前3天的变化规律,从第3天起,所排污水中硫化物的浓度![]() 与时间
与时间![]() 成反比例关系
成反比例关系
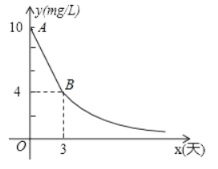
(1)求整改过程中硫化物的浓度![]() 与时间
与时间![]() 的函数表达式(要求标注自变量
的函数表达式(要求标注自变量![]() 的取值范围)
的取值范围)
(2)该企业所排污水中硫化物的浓度,能否在15天以内(含15天)排污达标?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线l和l外一点C.
求作:经过点C且垂直于l的直线.
作法:如图,
(1)在直线l上任取点A;
(2)以点C为圆心,AC为半径作圆,交直线l于点B;
(3)分别以点A,B为圆心,大于![]() 的长为半径作弧,两弧相交于点D;
的长为半径作弧,两弧相交于点D;
(4)作直线CD.
所以直线CD就是所求作的垂线.
(1)请使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明.
证明:连接AC,BC,AD,BD.
∵AC=BC, = ,
∴CD⊥AB(依据: ).
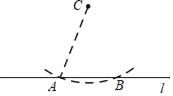
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=![]() (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.

(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
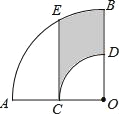
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交![]() 于点E,以点O为圆心,OC的长为半径作
于点E,以点O为圆心,OC的长为半径作![]() 交OB于点D.若OA=4,则图中阴影部分的面积为( )
交OB于点D.若OA=4,则图中阴影部分的面积为( )
A. ![]() +
+![]() B.
B. ![]() +2
+2![]() C.
C. ![]() +
+![]() D. 2
D. 2![]() +
+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com