
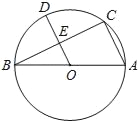
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E.
(1)求证:OD∥AC;
(2)若BC=8,DE=3,求⊙O的直径.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】某小区开展了“行车安全,方便居民”的活动,对地下车库作了改进.如图,这小区原地下车库的入口处有斜坡AC长为13米,它的坡度为i=1:2.4,AB⊥BC,为了居民行车安全,现将斜坡的坡角改为13°,即∠ADC=13°(此时点B、C、D在同一直线上).
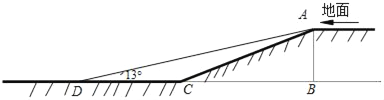
(1)求这个车库的高度AB;
(2)求斜坡改进后的起点D与原起点C的距离(结果精确到0.1米).
(参考数据:sin13°≈0.225,cos13°≈0.974,tan13°≈0.231,cot13°≈4.331)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在测量“河流宽度”的综合与实践活动中,小李同学设计的方案及测量数据如下:在河对岸边选定一个目标点A,在近岸取点B,C,D (点B,C,D在同一条直线上),AB⊥BD,∠ACB=45°,CD=20米,且.若测得∠ADB=25°,请你帮助小李求河的宽度AB.(sin25°≈0.42,cos25°≈0.91,tan25°≈0.47,结果精确到0.1米).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实国务院的指示精神,某地方政府出台了一系列“三农”优惠政策,使农民收入大幅度增加.某农户生产经销一种农产品,已知这种产品的成本价为每千克20元,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)有如下关系:y=﹣2x+80.设这种产品每天的销售利润为w元.
(1)求w与x之间的函数关系式.
(2)该产品销售价定为每千克多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种产品的销售价不高于每千克28元,该农户想要每天获得150元的销售利润,销售价应定为每千克多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
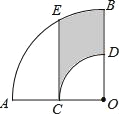
【题目】如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交![]() 于点E,以点O为圆心,OC的长为半径作
于点E,以点O为圆心,OC的长为半径作![]() 交OB于点D.若OA=4,则图中阴影部分的面积为( )
交OB于点D.若OA=4,则图中阴影部分的面积为( )
A. ![]() +
+![]() B.
B. ![]() +2
+2![]() C.
C. ![]() +
+![]() D. 2
D. 2![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图是一个组合几何体,右边是它的两种视图,在右边横线上填写出两种视图的名称;

视图 视图
(2)根据两种视图中尺寸(单位:cm),计算这个组合几何体的表面积.(π取3.14)
查看答案和解析>>
科目:初中数学 来源: 题型:
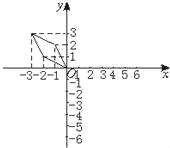
【题目】(1)将下图中的各个点的纵坐标不变,横坐标都乘﹣1,与原图案相比,所得图案有什么变化?请画出图形并写出结论;
(2)将下图中的各个点的横坐标不变,纵坐标都乘以-1,与原图案相比,所得图案有什么变化?请画出图形并写出结论;
(3)将下图中的各个点的横坐标不变,纵坐标都+3,与原图案相比,所得图案有什么变化?请画出图形并写出结论;
(4)将下图中的各个点的横坐标﹣2,纵坐标不变,与原图案相比,所得图案有什么变化?请画出图形并写出结论;
(5)将下图中的各个点的横坐标都乘2,纵坐标都乘2,与原图案相比,所得图案有什么变化?请画出图形并写出结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com