
【题目】如图,已知⊙O半径为10cm,弦AB垂直平分半径OC,并交OC于点D.
(1)求弦AB的长;
(2)求弧AB的长,并求出图中阴影部分面积.

【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先利用垂径定理得出AB=2BD,∠ODB=90°,OD=![]() OC=5,进而根据勾股定理求出BD,即可得出结论;
OC=5,进而根据勾股定理求出BD,即可得出结论;
(2)先利用锐角三角函数求出∠BOD=60°,最后利用扇形的弧长公式和扇形的面积公式即可得出结论.
解:(1)如图,⊙O半径为10cm,
∴OB=OC=10,
∵弦AB垂直平分半径OC,
∴AB=2BD,∠ODB=90°,OD=![]() OC=5,
OC=5,
在Rt△BOD中,根据勾股定理得,BD=![]() =5
=5![]() ,
,
∴AB=2BD=10![]() cm;
cm;
(2)由(1)知,OD=5,
在Rt△BOD中,cos∠BOD=![]() =
=![]() ,
,
∴∠BOD=60°,
∵OC⊥AB,
∴∠AOB=2∠BOD=120°,
∴l弧AB=![]() =
=![]() =
=![]() cm,
cm,
S阴影=S扇形AOB﹣S△AOB=![]() ﹣
﹣![]() AB×OD=
AB×OD=![]() ﹣
﹣![]() ×10
×10![]() ×5=
×5=![]() ﹣25
﹣25![]() (cm2).
(cm2).


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.

(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.M在AB上,且∠APM=∠APD,过点B作BN∥MP交DC于点N.
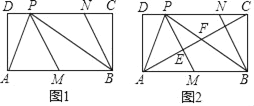
(1)求证:四边形PMBN是菱形;
(2)求证:ADBC=DPPC;
(3)如图2,连接AC,分别交PM,PB于点E,F,若DP=1,AD=2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
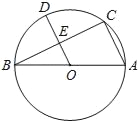
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,连接BC,AC,OD⊥BC于E.
(1)求证:OD∥AC;
(2)若BC=8,DE=3,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
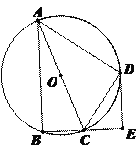
【题目】如图,四边形ABCD是⊙O的内接四边形, ![]() ,AC为直径, DE⊥BC,垂足为E.
,AC为直径, DE⊥BC,垂足为E.
(1)求证:CD平分∠ACE;
(2)若AC=9,CE=3,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学运动队有短跑、长跑、跳远、实心球四个训练小队,现将四个训练小队队员情况绘制成如下不完整的统计图:
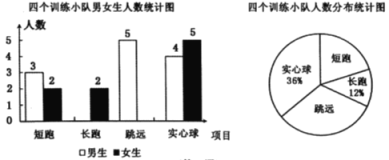
(l)学校运动队的队员总人数为 人,扇形统计图中短跑训练小队所对应圆心角的度数为 ;
(2)补全条形统计图,并标明数据;
(3)若在短跑训练小组中随机选取2名同学进行比赛,请用列举法(画树状图或列表)求所选取的这两名同学恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
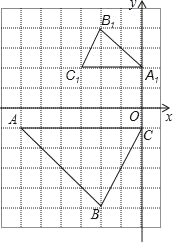
【题目】如图,△ABC与△A1B1C1是位似图形.
(1)在网格上建立平面直角坐标系,使得点A的坐标为(﹣6,﹣1),点C1的坐标为(﹣3,2),则点B的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2;
(3)在图上标出△ABC与△A1B1C1的位似中心P,并写出点P的坐标为 ,计算四边形ABCP的周长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
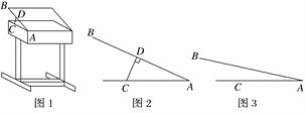
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com