
����Ŀ��ij��ѧ�˶����ж��ܡ����ܡ���Զ��ʵ�����ĸ�ѵ��С�ӣ��ֽ��ĸ�ѵ��С�Ӷ�Ա������Ƴ����²�������ͳ��ͼ:
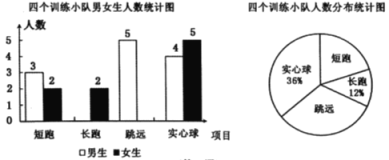
(l)ѧУ�˶��ӵĶ�Ա������Ϊ �ˣ�����ͳ��ͼ�ж���ѵ��С������ӦԲ�ĽǵĶ���Ϊ ;
(2)��ȫ����ͳ��ͼ������������;
(3)���ڶ���ѵ��С�������ѡȡ2��ͬѧ���б����������оٷ�(����״ͼ���б�)����ѡȡ��������ͬѧǡ����һ��һŮ�ĸ���.
���𰸡���1��25.72����2����������1�ˣ���ԶŮ��3�ˣ���3��![]() .
.
��������
��1����������5+4����36%=25���ˣ���Բ�Ľǣ�![]() ����2�����б��������.
����2������������.
�⣺��1����������5+4����36%=25���ˣ���Բ�Ľǣ�![]()
��2���б�
��1 | ��2 | ��3 | Ů1 | Ů2 | ||||||
��1 | ��1 | ��2 | ��1 | ��3 | ��1 | Ů1 | ��1 | Ů2 | ||
��2 | ��2 | ��1 | ��2 | ��3 | ��2 | Ů1 | ��2 | Ů2 | ||
��3 | ��3 | ��1 | ��3 | ��2 | ��3 | Ů1 | ��3 | Ů2 | ||
Ů1 | Ů1 | ��1 | Ů1 | ��2 | Ů1 | ��3 | Ů1 | Ů2 | ||
Ů2 | Ů2 | ��1 | Ů2 | ��2 | Ů2 | ��3 | Ů2 | Ů1 | ||
���ԣ�P��ǡ��һ��һŮ��=![]()


 ��������ܸ�ϰϵ�д�
��������ܸ�ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ֱ��l��l��һ��C��
������������C�Ҵ�ֱ��l��ֱ�ߣ�
��������ͼ��
��1����ֱ��l����ȡ��A��
��2���Ե�CΪԲ�ģ�ACΪ�뾶��Բ����ֱ��l�ڵ�B��
��3���ֱ��Ե�A��BΪԲ�ģ�����![]() �ij�Ϊ�뾶�����������ཻ�ڵ�D��
�ij�Ϊ�뾶�����������ཻ�ڵ�D��
��4����ֱ��CD��
����ֱ��CD�����������Ĵ��ߣ�
��1����ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ�������ͼ�ۼ�����
��2����������֤����
֤��������AC��BC��AD��BD��
��AC��BC���� ������ ����
��CD��AB�����ݣ��� ������
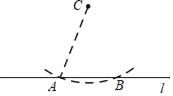
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڲ������������������ۺ���ʵ����У�С��ͬѧ��Ƶķ����������������£��ںӶ���ѡ��һ��Ŀ���A���ڽ���ȡ��B��C��D (��B��C��D��ͬһ��ֱ����)��AB��BD����ACB��45�㣬CD��20�ף��ң�����á�ADB��25�����������С����ӵĿ���AB.��sin25���0.42��cos25���0.91��tan25���0.47�������ȷ��0.1�ף���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
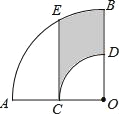
����Ŀ����ͼ��������AOB�У���AOB=90������CΪOA���е㣬CE��OA��![]() �ڵ�E���Ե�OΪԲ�ģ�OC�ij�Ϊ�뾶��
�ڵ�E���Ե�OΪԲ�ģ�OC�ij�Ϊ�뾶��![]() ��OB�ڵ�D����OA=4����ͼ����Ӱ���ֵ����Ϊ��������
��OB�ڵ�D����OA=4����ͼ����Ӱ���ֵ����Ϊ��������
A. ![]() +
+![]() B.
B. ![]() +2
+2![]() C.
C. ![]() +
+![]() D. 2
D. 2![]() +
+![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��O�뾶Ϊ10cm����AB��ֱƽ�ְ뾶OC������OC�ڵ�D��
��1������AB�ij���
��2����AB�ij��������ͼ����Ӱ���������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
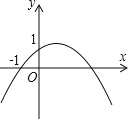
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ��Ķ����ڵ�һ���ޣ��ҹ��㣨0��1���ͣ���1��0�������н��ۣ���ab��0����b2��4a����0��a+b+c��2����0��b��1������x����1ʱ��y��0��������ȷ���۵ĸ�����
A��5�� B��4�� C��3�� D��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��ͼ��һ����ϼ����壬�ұ�������������ͼ�����ұߺ�������д��������ͼ�����ƣ�

������������������������ ��ͼ������������ ��ͼ
(2)����������ͼ�гߴ�(��λ��cm)�����������ϼ�����ı������(��ȡ3.14)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳���Ϊ�������˿ͣ�������ɫ���˽�������ٰ�����Ʒ�н���������������200Ԫ�ߣ������ֽ���������ѡ��һ��ֱ�ӻ��20Ԫ�����ȯ�����ǵõ�һ��ҡ���Ļ��ᣮ��֪��ҡ������װ��2�������2��������ɫ����������ͬ��ҡ���߱����ҡ������һ������ҡ���������������ɫ����������������ȯ�Ķ��٣�
�� | ���� | һ��һ�� | ���� |
���ȯ��Ԫ�� | 18 | 24 | 18 |
��1���������б���������״ͼ������һ������ҡ��һ��һ������ĸ��ʣ�
��2�����һ���˿͵����ڱ��깺����200Ԫ����ֻ���ǻ��������Ʒȯ�������������ѡ�����ַ�����Ϊʵ�ݣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijˮ��������ij��ˮ�����������г������֪���ӵ�1������12�£�����ˮ��ÿǧ���ۼ�y1��Ԫ��������ʱ���x��֮�������ͼ1��һ���߶Σ��ı仯���ƣ�ÿǧ�˳ɱ�y2��Ԫ��������ʱ���x�����㺯����ϵʽy2=mx2��8mx+n����仯������ͼ2��
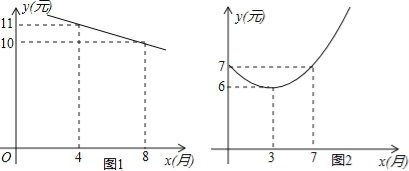
��1����y2�Ľ���ʽ��
��2���ڼ�����������ˮ����ÿǧ����������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com