
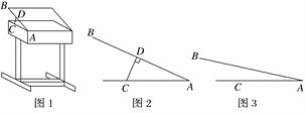
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
【答案】解:(1)在Rt△ADC中,AC=30,∠DAC=24°,sin∠DAC=![]() ,
,
∴DC=AC·sin∠DAC ≈30×0.40=12.…………………………3分
答:支撑臂DC的长为12 cm.
(2)本题分两种情况,
过点C作CE⊥AB,垂足为E.
在Rt△ACE中,AC=30,∠EAC=12°,sin∠EAC=![]() ,
,
∴CE=AC·sin∠EAC ≈30×0.20=6.…………………………4分
【解析】
(1)∵在Rt△ADC中,AC=30,∠DAC=24°,Sin∠DAC=![]()
∴DC=AC·Sin∠DAC=30×0.40=12
答:支撑臂CD的长为12. …………………………………2分
(2)本题分两种情况。
过C作CE⊥AB,垂足为E.
在Rt△ACE中,AC="30," ∠EAC=12°,Sin∠EAC=![]()
∴CE=AC·Sin∠EAC=30×0.20=6
∴AE=![]()
∵在Rt△EDC中,DC=12,CE=6,
∴DE=![]() ………………………4分
………………………4分
∴AD=12±![]() …………………………………………………………6分
…………………………………………………………6分


科目:初中数学 来源: 题型:
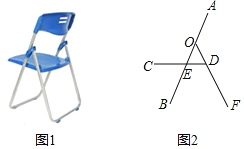
【题目】如图1,是一种折叠椅,忽略其支架等的宽度,得到它的侧面简化结构图(图2),支架与坐板均用线段表示.若坐板CD平行于地面,前支撑架AB与后支撑架OF分别与CD交于点E,D,ED=25cm,OD=20cm,DF=40cm,∠ODC=60°,∠AED=50°.
(1)求两支架着地点B,F之间的距离;
(2)若A、D两点所在的直线正好与地面垂直,求椅子的高度.
(结果取整数,参数数据:sin60°=0.87,cos60°=0.5,tan60°=1.73,sin50°=0.77,cos50°=0.64,tan50°=1.19)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图为水平放置于桌面上的台灯的示意图,已知灯臂AB=18cm,灯罩BC=30cm,∠BAM=60°,∠ABC=90°,求点C到桌面的距离CD(精确到0.1cm).参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73.
≈1.73.
查看答案和解析>>
科目:初中数学 来源: 题型:
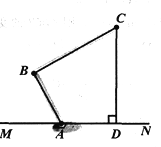
【题目】如图,一垂直于地面的灯柱AB被一钢筋CD固定,CD与地面成45°夹角(∠CDB=45°),在C点上方2米处加固另一条钢线ED,ED与地面成53°夹角(∠EDB=53°),那么钢线ED的长度约为多少米?(结果精确到1米,参考数据:sin53°≈0.80,cos53°≈0.60,tan53°≈1.33)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)化简![]() ;
;
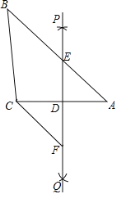
(2)如图,已知△ABC,按如下步骤作图:
①分别以A,C为圆心,大于![]() AC的长为半径画弧,两弧交于P, Q两点;
AC的长为半径画弧,两弧交于P, Q两点;
②作直线PQ,分别交AB,AC于点E,D;
③过C作CF∥AB交PQ于点F.
求证:△AED≌△CFD;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 和二次函数
和二次函数![]() 图象的顶点分别为M、N ,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边),
图象的顶点分别为M、N ,与x轴分别相交于A、B两点(点A在点B的左边)和C、D两点(点C在点D的左边),
(1))函数![]() 的顶点坐标为 ;当二次函数L1 ,L2 的
的顶点坐标为 ;当二次函数L1 ,L2 的![]() 值同时随着
值同时随着![]() 的增大而增大时,
的增大而增大时,![]() 的取值范围是 ;
的取值范围是 ;
(2)当AD=MN时,求![]() 的值,并判断四边形AMDN的形状(直接写出,不必证明);
的值,并判断四边形AMDN的形状(直接写出,不必证明);
(3)当B,C是线段AD的三等分点时,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,则AF的最小值是_____.
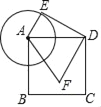
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=﹣x2+2x+3经过点A、C、A′三点.
(1)求A、A′、C三点的坐标;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;
(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M的坐标.
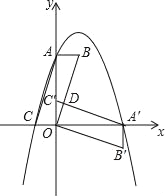
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com