
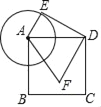
【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,则AF的最小值是_____.
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2; ②3a+c>0;③方程
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2; ②3a+c>0;③方程![]() 的两个根是x1=﹣1,x2=3;④当y>0时,x的取值范围是﹣1<x<3⑤当x>0时,y随x的增大而减小.其中结论正确的个数是( )
的两个根是x1=﹣1,x2=3;④当y>0时,x的取值范围是﹣1<x<3⑤当x>0时,y随x的增大而减小.其中结论正确的个数是( )
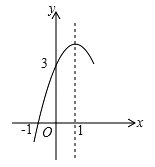
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A,B,C,表示的数分别是﹣4,﹣2,3.
![]()
(1)若使C、B两点的距离是A、B两点的距离的2倍,则需将点C向左移动 个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒a个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t秒:
①点A、B、C表示的数分别是 、 、 (用含a、t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2,当a为何值时,5d1﹣3d2的值不会随着时间t的变化而改变,并求此时5d1﹣3d2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间,文具店老板购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
型号 | 进价(元/只) | 售价(元/只) |
A型 | 10 | 14 |
B型 | 15 | 22 |
(1)老板如何进货,能使进货款恰好为1350元?
(2)要使销售文具所获利润不少于500元,那么老板最多能购进A型文具多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在△ABC中,D在AB边上,DE⊥BC于E,∠A=2∠BDE.
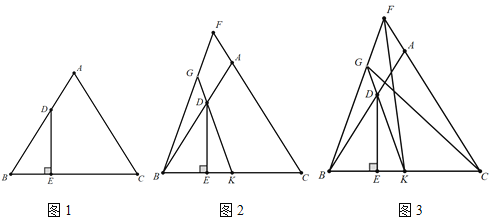
(1)求证:AB=AC;
(2)延长CA至F,连接BF,G在线段BF上,连接DG,∠F=∠BDK,延长GD交BC于K,如图2,试判断线段KG与BG的数量关系,并加以证明;
(3)在(2)的条件下,连接CG、FK,CG=FK,∠CGK=∠BFK,FG=2,CK=3,如图3,求线段BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,若△CEF的面积为18cm2,则S△DGF等于( )
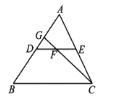
A.4cm2B.5cm2C.6cm2D.7 cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
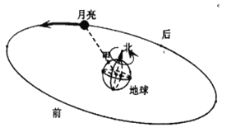
【题目】如果把月亮绕地球旋转的轨迹看成一个圆,地心在圆心上。我们知道地球每24小时逆时针方向自转一圈(从俯视角度看),月亮每月逆时针绕地球旋转一圈.
(1)求地球每小时旋转的角度;
(2)求月亮绕地球每小时旋转的角度(每月以30天记);
(3)某月15日20:00时,月亮恰好在甲地正上方(如图),到第二天大约几时几分月亮再次出现在甲地正上方?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.
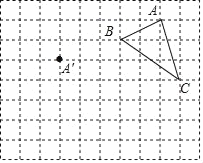
(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生态公园计划在园内的坡地上造一片有![]() 、
、![]() 两种树的混合林,需要购买这两种树苗2000棵,种植
两种树的混合林,需要购买这两种树苗2000棵,种植![]() 、
、![]() 两种树苗的相关信息如下表:
两种树苗的相关信息如下表:
品名 | 单价(元/棵) | 栽树劳务费(元/棵) | 成活率 |
| 25 | 3 |
|
| 30 | 4 |
|
设购买![]() 种树苗
种树苗![]() 棵,解答下列问题:
棵,解答下列问题:
(1)购买的![]() 种树苗的数量为_______棵(含
种树苗的数量为_______棵(含![]() 的代数式表示);
的代数式表示);
(2)请用含![]() 的代数式表示造这片林的总费用;
的代数式表示造这片林的总费用;
(3)假设这批树苗种植后成活1960棵,则造这片林的总费用需多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com