
【题目】如图1在△ABC中,D在AB边上,DE⊥BC于E,∠A=2∠BDE.
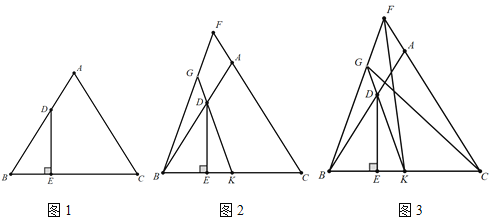
(1)求证:AB=AC;
(2)延长CA至F,连接BF,G在线段BF上,连接DG,∠F=∠BDK,延长GD交BC于K,如图2,试判断线段KG与BG的数量关系,并加以证明;
(3)在(2)的条件下,连接CG、FK,CG=FK,∠CGK=∠BFK,FG=2,CK=3,如图3,求线段BF的长度.
【答案】(1)见解析;(2)KG=BG,证明见解析;(3)BF=6.5.
【解析】
(1)过A作AM⊥BC于M可推DE∥AM可得∠3=∠2,推出∠B=∠C得出结论;
(2)由∠ABC=∠ACB及∠F=∠BDK可得∠GKB=∠GBK,由三角形内角和可得∠BKD=∠FBK可推出BG=GK
(3)延长GK至M使KM=FG=2可证△BFK≌△MGC,可得BK=CM,∠GBK=∠BKG=∠CKM=∠CMK,可得△BGK≌△MCK,所以![]() ,推出BG=4.5,所以BF=BG+FG=6.5
,推出BG=4.5,所以BF=BG+FG=6.5
(1)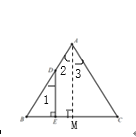
过A作AM⊥BC于M
∵AM⊥BC,DE⊥BC
∴∠DEB=∠AMB=90°,∠AMB=∠AMC=90°
∴DE∥AM
∴∠1=∠2
∵∠BAC=2∠1
∴∠BAC=2∠2
∴∠3=∠2
∴∠B=90°-∠2,∠C=90°-∠3
∴∠B=∠C
∴AB=AC
(2)∵AB=AC
∴∠ABC=∠ACB
∵∠F=∠BDK
∴∠GKB=∠GBK
∵∠DBK+∠BDK+∠BKD=180°
又∵∠BCF+∠F+∠FBK=180°
∴∠BKD=∠FBK
∴BG=GK
(3)
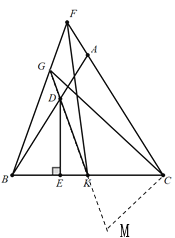
延长GK至M使KM=FG=2
∵BG=GK
∴BG+FG=KM+GK
即BF=MG
又∵∠BFK=∠MGC,FK=GC
∴△BFK≌△MGC
∴∠GBK=∠M,BK=CM
∵∠GBK=∠GKB,∠CKM=∠BKG
∴∠GBK=∠BKG=∠CKM=∠CMK
∴CM=CK=3
∴BK=3
∵∠GBK=∠CMK,∠GKB=∠MKC
∴![]()
∴![]()
∴![]()
∴BG=4.5
∴BF=BG+FG=6.5


科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的边
的边![]() 上有一动点
上有一动点![]() ,从距离
,从距离![]() 点
点![]() 的点
的点![]() 处出发,沿线段
处出发,沿线段![]() ,射线
,射线![]() 运动,速度为
运动,速度为![]() ;动点
;动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,速度为
运动,速度为![]() .
.![]() ,
,![]() 同时出发,设运动时间是
同时出发,设运动时间是![]() .
.

(1)当点![]() 在
在![]() 上运动时,
上运动时,![]()
![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 在
在![]() 上运动时,
上运动时,![]() 为何值,能使
为何值,能使![]() ?
?
(3)若点![]() 运动到距离
运动到距离![]() 点
点![]() 的点
的点![]() 处停止,在点
处停止,在点![]() 停止运动前,点
停止运动前,点![]() 能否追上点
能否追上点![]() ?如果能,求出
?如果能,求出![]() 的值;如果不能,请说出理由.
的值;如果不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣30|+(b+6)2=0.点O是数轴原点.
![]()
(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进A、B两种商品,若购进A种商品5件,B种商品3件,共需450元;若购进A种商品10件,B种商品8件,共需1000元.
(1)购进A、B两种商品每件各需多少元?
(2)该商店购进足够多的A、B两种商品,在销售中发现,A种商品售价为每件80元,每天可销售100件,现在决定对A种商品在每件80元的基础上降价销售,每件每降价1元,多售出20件,该商店对A种商品降价销售后每天销量超过200件;B种商品销售状况良好,每天可获利7000元,为使销售A、B两种商品每天总获利为10000元,A种商品每件降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为3,以点A为圆心,1为半径作圆,E是⊙A上的任意一点,将DE绕点D按逆时针旋转90°,得到DF,连接AF,则AF的最小值是_____.
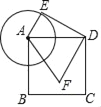
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润 2000元。
该加工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨。受人员限制,两种加工方式不可同时进行。受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多地制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
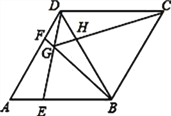
【题目】如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:①△AED≌△DFB; ②S四边形BCDG=![]() CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
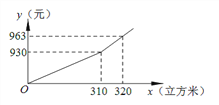
【题目】某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图像并回答下列问题:
(1)年用天然气量不超过310立方米时,求y关于x的函数解析式(不写定义域);
(2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com