
【题目】如图,![]() 的边
的边![]() 上有一动点
上有一动点![]() ,从距离
,从距离![]() 点
点![]() 的点
的点![]() 处出发,沿线段
处出发,沿线段![]() ,射线
,射线![]() 运动,速度为
运动,速度为![]() ;动点
;动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,速度为
运动,速度为![]() .
.![]() ,
,![]() 同时出发,设运动时间是
同时出发,设运动时间是![]() .
.

(1)当点![]() 在
在![]() 上运动时,
上运动时,![]()
![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 在
在![]() 上运动时,
上运动时,![]() 为何值,能使
为何值,能使![]() ?
?
(3)若点![]() 运动到距离
运动到距离![]() 点
点![]() 的点
的点![]() 处停止,在点
处停止,在点![]() 停止运动前,点
停止运动前,点![]() 能否追上点
能否追上点![]() ?如果能,求出
?如果能,求出![]() 的值;如果不能,请说出理由.
的值;如果不能,请说出理由.
【答案】(1)![]() ;(2)
;(2)![]() 时,能使
时,能使![]() ;(3) 不能,理由见解析
;(3) 不能,理由见解析
【解析】
(1)利用P点运动速度以及OM的距离进而得出答案;
(2)利用OP=OQ列出方程求解即可;
(3)设t秒时点P追上点Q,根据“P的路程=18+Q的路程”列方程,求出所用时间,进而得出答案.
(1)∵P点运动速度为2cm/s,MO=18cm,
∴当点P在MO上运动时,PO=(18﹣2t)cm.
故答案为:(18﹣2t);
(2)当OP=OQ时,则有18﹣2t=t,
解这个方程,得:t=6,
即t=6时,能使OP=OQ;
(3)不能.理由如下:
设t秒时点P追上点Q,则2t=t+18,
解这个方程,得:t=18,
即点P追上点Q需要18s,此时点Q已经停止运动,
∴在点Q停止运动前,点P不能追上点Q.


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=∠DOC=90°,OE平分∠AOD,反向延长射线OE至F.
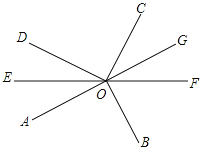
(1)∠AOD和∠BOC是否互补?说明理由;
(2)射线OF是∠BOC的平分线吗?说明理由;
(3)反向延长射线OA至点G,射线OG将∠COF分成了4:3的两个角,求∠AOD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=2cm.
![]()
(1)求AC的长
(2)若点E在直线AD上,且EA=3cm,求BE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两支“徒步队”到野外沿相同路线徒步,徒步的路程为24千米.甲队步行速度为4千米/时,乙队步行速度为6千米/时.甲队出发1小时后,乙队才出发,同时乙队派一名联络员跑步在两队之间来回进行一次联络(不停顿),他跑步的速度为10千米/时.
(1)乙队追上甲队需要多长时间?
(2)联络员从出发到与甲队联系上后返回乙队时,他跑步的总路程是多少?
(3)从甲队出发开始到乙队完成徒步路程时止,何时两队间间隔的路程为1千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有三个点A,B,C,表示的数分别是﹣4,﹣2,3.
![]()
(1)若使C、B两点的距离是A、B两点的距离的2倍,则需将点C向左移动 个单位;
(2)点A、B、C开始在数轴上运动,若点A以每秒a个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动,设运动时间为t秒:
①点A、B、C表示的数分别是 、 、 (用含a、t的代数式表示);
②若点B与点C之间的距离表示为d1,点A与点B之间的距离表示为d2,当a为何值时,5d1﹣3d2的值不会随着时间t的变化而改变,并求此时5d1﹣3d2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着互联网的发展,同学们的学习习惯也有了改变,一些同学在做题遇到困难时,喜欢上网查找答案.针对这个问题,某校调查了部分学生对这种做法的意见(分为:赞成、无所谓、反对),并将调查结果绘制成图1和图2两个不完整的统计图.
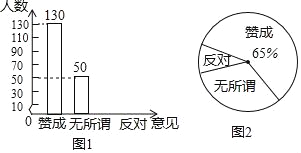
请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了多少名学生?
(2)将图1补充完整;
(3)求出扇形统计图中持“反对”意见的学生所在扇形的圆心角的度数;
(4)根据抽样调查结果,请你估计该校1500名学生中有多少名学生持“无所谓”意见.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在△ABC中,D在AB边上,DE⊥BC于E,∠A=2∠BDE.
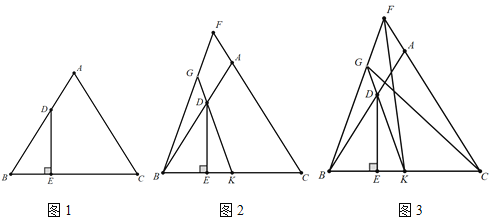
(1)求证:AB=AC;
(2)延长CA至F,连接BF,G在线段BF上,连接DG,∠F=∠BDK,延长GD交BC于K,如图2,试判断线段KG与BG的数量关系,并加以证明;
(3)在(2)的条件下,连接CG、FK,CG=FK,∠CGK=∠BFK,FG=2,CK=3,如图3,求线段BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,下列结论:
,下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ,
,
其中正确的有__________(只填序号).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com