
【题目】如图,在矩形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,下列结论:
,下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ,
,
其中正确的有__________(只填序号).

【答案】①②③④
【解析】
①根据角平分线的定义可得∠BAE=∠DAE=45°,然后利用求出△ABE是等腰直角三角形,根据等腰直角三角形的性质可得AE=![]() AB,从而得到AE=AD,然后利用“角角边”证明△ABE和△AHD全等,根据全等三角形对应边相等可得BE=DH,再根据等腰三角形两底角相等求出∠ADE=∠AED=67.5°,根据平角等于180°求出∠CED=67.5°,从而判断出①正确;②求出∠AHB=67.5°,∠DHO=∠ODH=22.5°,然后根据等角对等边可得OE=OD=OH,判断出②正确;③求出∠EBH=∠OHD=22.5°,∠AEB=∠HDF=45°,然后利用“角边角”证明△BEH和△HDF全等,根据全等三角形对应边相等可得BH=HF,判断出③正确;④根据全等三角形对应边相等可得DF=HE,然后根据HE=AE-AH=BC-CD,BC-CF =BC-(CD-DF)=2HE,判断出④正确;⑤判断出△ABH不是等边三角形,从而得到AB≠BH,即AB≠HF,得到⑤错误.
AB,从而得到AE=AD,然后利用“角角边”证明△ABE和△AHD全等,根据全等三角形对应边相等可得BE=DH,再根据等腰三角形两底角相等求出∠ADE=∠AED=67.5°,根据平角等于180°求出∠CED=67.5°,从而判断出①正确;②求出∠AHB=67.5°,∠DHO=∠ODH=22.5°,然后根据等角对等边可得OE=OD=OH,判断出②正确;③求出∠EBH=∠OHD=22.5°,∠AEB=∠HDF=45°,然后利用“角边角”证明△BEH和△HDF全等,根据全等三角形对应边相等可得BH=HF,判断出③正确;④根据全等三角形对应边相等可得DF=HE,然后根据HE=AE-AH=BC-CD,BC-CF =BC-(CD-DF)=2HE,判断出④正确;⑤判断出△ABH不是等边三角形,从而得到AB≠BH,即AB≠HF,得到⑤错误.
∵在矩形ABCD中,AE平分∠BAD,
∴∠BAE=∠DAE=45°,
∴△ABE是等腰直角三角形,
∴AE=![]() AB,
AB,
∵AD=![]() AB,
AB,
∴AE=AD,
在△ABE和△AHD中,
∵∠BAE=∠DAE,
∠ABE=∠AHD=90°,
AE=AD,
∴△ABE≌△AHD(AAS),
∴BE=DH,
∴AB=BE=AH=HD,
∴∠ADE=∠AED=![]() (180°-45°)=67.5°,
(180°-45°)=67.5°,
∴∠CED=180°-45°-67.5°=67.5°,
∴∠AED=∠CED,故①正确;
∵AB=AH,
∵∠AHB=![]() (180°-45°)=67.5°,∠OHE=∠AHB(对顶角相等),
(180°-45°)=67.5°,∠OHE=∠AHB(对顶角相等),
∴∠OHE=67.5°=∠AED,
∴OE=OH,
∵∠DHO=90°-67.5°=22.5°,∠ODH=67.5°-45°=22.5°,
∴∠DHO=∠ODH,
∴OH=OD,
∴OE=OD=OH,故②正确;
∵∠EBH=90°-67.5°=22.5°,
∴∠EBH=∠OHD,
在△BEH和△HDF中,
∵∠EBH=∠OHD=22.5°,
BE=DH,
∠AEB=∠HDF=45°,
∴△BEH≌△HDF(ASA),
∴BH=HF,HE=DF,故③正确;
∵HE=AE-AH=BC-CD,
∴BC-CF=BC-(CD-DF)=BC-(CD-HE)
=(BC-CD)+HE=HE+HE=2HE.故④正确;
∵AB=AH,∠BAE=45°,
∴△ABH不是等边三角形,
∴AB≠BH,
∴即AB≠HF,故⑤错误;
综上所述,结论正确的是①②③④.
故答案为:①②③④.


科目:初中数学 来源: 题型:
【题目】如图,![]() 的边
的边![]() 上有一动点
上有一动点![]() ,从距离
,从距离![]() 点
点![]() 的点
的点![]() 处出发,沿线段
处出发,沿线段![]() ,射线
,射线![]() 运动,速度为
运动,速度为![]() ;动点
;动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 运动,速度为
运动,速度为![]() .
.![]() ,
,![]() 同时出发,设运动时间是
同时出发,设运动时间是![]() .
.

(1)当点![]() 在
在![]() 上运动时,
上运动时,![]()
![]() (用含
(用含![]() 的代数式表示);
的代数式表示);
(2)当点![]() 在
在![]() 上运动时,
上运动时,![]() 为何值,能使
为何值,能使![]() ?
?
(3)若点![]() 运动到距离
运动到距离![]() 点
点![]() 的点
的点![]() 处停止,在点
处停止,在点![]() 停止运动前,点
停止运动前,点![]() 能否追上点
能否追上点![]() ?如果能,求出
?如果能,求出![]() 的值;如果不能,请说出理由.
的值;如果不能,请说出理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润 2000元。
该加工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨。受人员限制,两种加工方式不可同时进行。受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多地制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
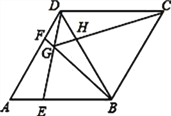
【题目】如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:①△AED≌△DFB; ②S四边形BCDG=![]() CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由![]() 个完全相同的小正方体搭成的物体如图所示.
个完全相同的小正方体搭成的物体如图所示.
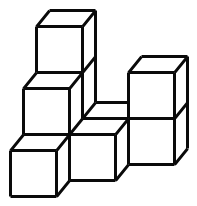
(1)请在下面的方格图中画出该物体的主视图和左视图;
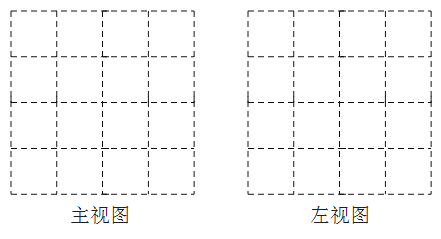
(2)如果再添加若干个相同的小正方体之后,所得到的新物体的主视图和左视图跟原来的相间,那么这样的小正方体最多还可以添加 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
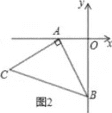
【题目】如图1,![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
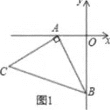
(1)求![]() 点的坐标;
点的坐标;
(2)如图2,在平面内是否存在一点![]() ,使得以
,使得以![]() 为顶点的四边形为平行四边形?若存在,请写出
为顶点的四边形为平行四边形?若存在,请写出![]() 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
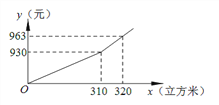
【题目】某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图像并回答下列问题:
(1)年用天然气量不超过310立方米时,求y关于x的函数解析式(不写定义域);
(2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.
查看答案和解析>>
科目:初中数学 来源: 题型:
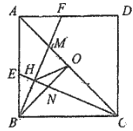
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 上的点,
上的点,![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有( )
.其中正确的结论有( )
A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com