
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
【答案】(1)四边形EFGH的形状是平行四边形.理由见解析;(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.(3)矩形.
【解析】
试题解析:(1)连接BD,根据三角形的中位线定理得到EH∥BD,EH=![]() BD,FG∥BD,FG=
BD,FG∥BD,FG=![]() BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
BD,推出,EH∥FG,EH=FG,根据一组对边平行且相等的四边形是平行四边形得出四边形EFGH是平行四边形;
(2)根据有一个角是直角的平行四边形是矩形,可知当四边形ABCD的对角线满足AC⊥BD的条件时,四边形EFGH是矩形;
(3)菱形的中点四边形是矩形.根据三角形的中位线平行于第三边并且等于第三边的一半可得EH∥BD,EF∥AC,再根据矩形的每一个角都是直角可得∠1=90°,然后根据平行线的性质求出∠3=90°,再根据垂直定义解答.
试题解析:(1)四边形EFGH的形状是平行四边形.理由如下:
如图,连结BD.
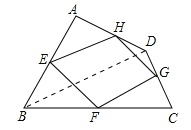
∵E、H分别是AB、AD中点,
∴EH∥BD,EH=![]() BD,
BD,
同理FG∥BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形;
(2)当四边形ABCD的对角线满足互相垂直的条件时,四边形EFGH是矩形.理由如下:
如图,连结AC、BD.

∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,
∵AC⊥BD,
∴EH⊥HG,
又∵四边形EFGH是平行四边形,
∴平行四边形EFGH是矩形;
(3)菱形的中点四边形是矩形.理由如下:
如图,连结AC、BD.
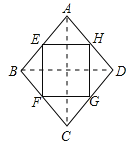
∵E、F、G、H分别为四边形ABCD四条边上的中点,
∴EH∥BD,HG∥AC,FG∥BD,EH=![]() BD,FG=
BD,FG=![]() BD,
BD,
∴EH∥FG,EH=FG,
∴四边形EFGH是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,
∵EH∥BD,HG∥AC,
∴EH⊥HG,
∴平行四边形EFGH是矩形.


科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 相等的角是对顶角; B. a、b、c是直线,若a//b,b//c,则a//c;
C. 同位角相等; D. a、b、c是直线,若a⊥b,b⊥c,则a⊥c。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地市话的收费标准为:
①通话时间在3分钟以内(包括3分钟)话费0.5元;
②通话时间超过3分钟时,超过部分的话费按每分钟0.15元计算.
在一次通话中,如果通话时间超过3分钟,那么话费y(元)与通话时间x(分)之间的关系式为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
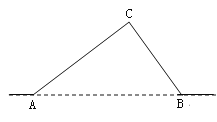
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(精确到0.1)
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com