
【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
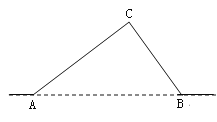
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(精确到0.1)
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
【答案】(1)14.7千米;(2)2.3千米.
【解析】
试题分析:(1)作CH⊥AB于点H,根据Rt△ACH的三角函数得出CH和AH的长度,然后根据Rt△BCH得出BH的长度,从而得到AB的长度;(2)首先求出BC的长度,然后根据AC+BC-AB得出答案.
试题解析:(1)作CH⊥AB于点H,在RT△ACH中 CH=AC·sin∠CAB= AC·sin25°=10×0.42=4.2
AH=AC·cos∠CAB= AC·cos25°=10×0.91=9.1
在RT△BCH中,
BH=CH÷tan37°=4.2÷0.75=5.6
∴AB=AH+BH=9.1+5.6=14.7(千米)
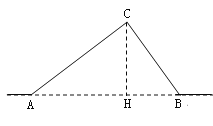
(2)BC=CH÷sin37°=4.2÷0.6=7.0
∴AC+BC-AB=10+7-14.7=2.3(千米)
答:公路改直后比原来缩短了2.3千米.


科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将□OABC放置在平面直角坐标系xOy内,已知AB边所在直线的函数解析式为:y=-x+4.若将□OABC绕点O逆时针旋转90°得OBDE,BD交OC于点P.
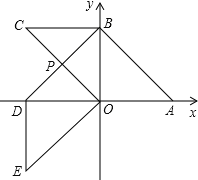
(1)直接写出点C的坐标是 :
(2)若再将四边形OBDE沿y轴正方向平移,设平移的距离为x(0≤x≤8),与□OABC重叠部分周长为L,试求出L关于x的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织全体学生参加了“走出校门,服务社会”的活动,活动分为打扫街道,去敬老院服务和到社区文艺演出三项.从七年级参加活动的同学中抽取了部分同学,对打扫街道,去敬老院服务和到社区文艺演出的人数进行了统计,并绘制了直方图和扇形统计图.请解决以下问题:
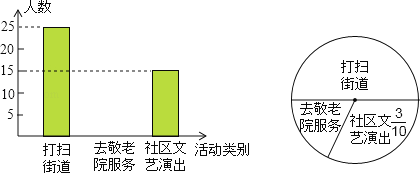
(1)求抽取的部分同学的人数;
(2)补全直方图的空缺部分;
(3)若七年级有200名学生,估计该年级去敬老院的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了检查一批零件的质量,从中抽取10件,测得它们的长度,下列叙述正确的是( )
A. 这一批零件的质量全体是总体 B. 从中抽取的10件零件是总体的一个样本
C. 这一批零件的长度的全体是总体 D. 每一个零件的质量为个体
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
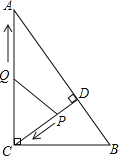
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得
S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,则说明理由.
(3)是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.
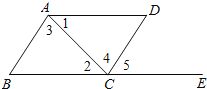
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com