
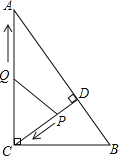
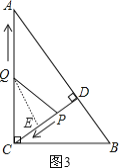
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得
S△CPQ:S△ABC=9:100?若存在,求出t的值;若不存在,则说明理由.
(3)是否存在某一时刻t,使得△CPQ为等腰三角形?若存在,求出所有满足条件的t的值;若不存在,则说明理由.
【答案】(1)4.8;(2)t=![]() 或t=3;(3)t=2.4秒或
或t=3;(3)t=2.4秒或![]() 秒或
秒或![]() 秒.
秒.
【解析】
试题分析:(1)根据勾股定理得出AB的长度,利用等面积法求出线段CD的长度;(2)过点P⊥PH⊥AC,根据题意得出DP=t,CQ=t,则CP=4.8-t,根据△CHP∽△BCA得出PH的长度,然后求出△CPQ与t的函数关系式,然后根据三角形的面积之比得出答案;(3)本题分CQ=CP、PQ=PC以及QC=QP三种情况得出答案.
试题解析:(1)如图1, ∵∠ACB=90°,AC=8,BC=6,
∴AB=10. ∵CD⊥AB,
∴S△ABC=![]() BCAC=
BCAC=![]() ABCD.
ABCD.
∴CD=![]() =
=![]() =4.8.
=4.8.
∴线段CD的长为4.8.
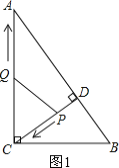
(2)过点P作PH⊥AC,垂足为H,如图2所示.
由题可知DP=t,CQ=t. 则CP=4.8﹣t.
∵∠ACB=∠CDB=90°,
∴∠HCP=90°﹣∠DCB=∠B.
∵PH⊥AC,
∴∠CHP=90°.
∴∠CHP=∠ACB.
∴△CHP∽△BCA.
∴![]() . ∴
. ∴![]() .
.
∴PH=![]() ﹣
﹣![]() t.
t.
∴S△CPQ=![]() CQPH=
CQPH=![]() t(
t(![]() ﹣
﹣![]() t)=﹣
t)=﹣![]() t2+
t2+![]() t.
t.
存在某一时刻t,使得S△CPQ:S△ABC=9:100.
∵S△ABC=![]() ×6×8=24,
×6×8=24,
且S△CPQ:S△ABC=9:100,
∴(﹣![]() t2+
t2+![]() t):24=9:100.
t):24=9:100.
整理得:5t2﹣24t+27=0.
即(5t﹣9)(t﹣3)=0.
解得:t=![]() 或t=3.
或t=3.
∵0≤t≤4.8,
∴当t=![]() 秒或t=3秒时,S△CPQ:S△ABC=9:100.
秒或t=3秒时,S△CPQ:S△ABC=9:100.
(3)存在
①若CQ=CP,如图1,则t=4.8﹣t.
解得:t=2.4
②若PQ=PC,如图2所示.
∵PQ=PC,PH⊥QC,
∴QH=CH=![]() QC=
QC=![]() .
.
∵△CHP∽△BCA.
∴![]() .
.
∴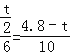 .
.
解得;t=![]() .
.
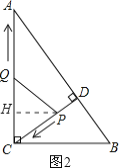
③若QC=QP,过点Q作QE⊥CP,垂足为E,如图3所示
同理可得:t=![]() .
.
综上所述:当t为2.4秒或![]() 秒或
秒或![]() 秒时,△CPQ为等腰三角形.
秒时,△CPQ为等腰三角形.


科目:初中数学 来源: 题型:
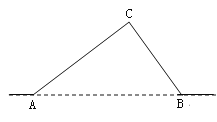
【题目】如图,从A地到B地的公路需经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°.因城市规划的需要,将在A、B两地之间修建一条笔直的公路.
(1)求改直后的公路AB的长;
(2)问公路改直后该段路程比原来缩短了多少千米?(精确到0.1)
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生态文明贵阳国际论坛作为我国目前唯一以生态文明为主题的国家级国际性论坛,现已被纳入国家“一带一路”总体规划,持续四届的成功举办,已相继吸引近7000名各国政要及嘉宾出席,7000这个数用科学记数法可表示为( )
A.70×102
B.7×103
C.0.7×104
D.7×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,以
中,以![]() 为直径作半圆,
为直径作半圆,![]() .现有两动点
.现有两动点![]() 、
、![]() ,分别从点
,分别从点![]() 、点
、点![]() 同时出发,点
同时出发,点![]() 沿线段
沿线段![]() 以
以![]() /秒的速度向点
/秒的速度向点![]() 运动,点
运动,点![]() 沿折线
沿折线![]() 以
以![]() /秒的速度向点
/秒的速度向点![]() 运动.当点
运动.当点![]() 到达
到达![]() 点时,
点时,![]() 、
、![]() 同时停止运动,设点
同时停止运动,设点![]() 运动时间为
运动时间为![]() .
.

(1)当![]() 为何值时,线段
为何值时,线段![]() 与
与![]() 平行?
平行?
(2)设![]() ,当
,当![]() 为何值时,
为何值时,![]() 与半圆相切?
与半圆相切?
(3)如图2,将图形放在直角坐标系中,当![]() 时,设
时,设![]() 与
与![]() 相交于点
相交于点![]() ,双曲线
,双曲线![]() 经过点
经过点![]() ,并且与边
,并且与边![]() 交于点
交于点![]() ,求出双曲线的函数关系式,并直接写出
,求出双曲线的函数关系式,并直接写出![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com