
【题目】如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:①△AED≌△DFB; ②S四边形BCDG=![]() CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
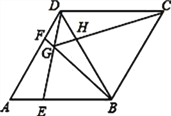
【答案】1 2 4
【解析】分析:(1)由已知条件易得∠A=∠BDF=60°,结合BD=AB=AD,AE=DF,即可证得△AED≌△DFB,从而说明结论①正确;(2)由已知条件可证点B、C、D、G四点共圆,从而可得∠CDN=∠CBM,如图,过点C作CM⊥BF于点M,过点C作CN⊥ED于点N,结合CB=CD即可证得△CBM≌△CDN,由此可得S四边形BCDG=S四边形CMGN=2S△CGN,在Rt△CGN中,由∠CGN=∠DBC=60°,∠CNG=90°可得GN=![]() CG,CN=
CG,CN=![]() CG,由此即可求得S△CGN=
CG,由此即可求得S△CGN=![]() CG2,从而可得结论②是正确的;(3)由已知易得△ADE中,∠AED>∠A=60°,从而可得AD>DE;在△DCG中,∠CDG>∠CGD=60°,从而可得CG>DC;结合AD=CD即可得到CG>DE,从而说明结论③错误;(4)过点F作FK∥AB交DE于点K,由此可得△DFK∽△DAE,△GFK∽△GBE,结合AF=2DF和相似三角形的性质即可证得结论④成立.
CG2,从而可得结论②是正确的;(3)由已知易得△ADE中,∠AED>∠A=60°,从而可得AD>DE;在△DCG中,∠CDG>∠CGD=60°,从而可得CG>DC;结合AD=CD即可得到CG>DE,从而说明结论③错误;(4)过点F作FK∥AB交DE于点K,由此可得△DFK∽△DAE,△GFK∽△GBE,结合AF=2DF和相似三角形的性质即可证得结论④成立.
详解:
(1)∵四边形ABCD是菱形,BD=AB,
∴AB=BD=BC=DC=DA,
∴△ABD和△CBD都是等边三角形,
∴∠A=∠BDF=60°,
又∵AE=DF,
∴△AED≌△DFB,即结论①正确;
(2)∵△AED≌△DFB,△ABD和△DBC是等边三角形,
∴∠ADE=∠DBF,∠DBC=∠CDB=∠BDA=60°,
∴∠GBC+∠CDG=∠DBF+∠DBC+∠CDB+∠GDB=∠DBC+∠CDB+∠GDB+∠ADE=∠DBC+∠CDB+∠BDA=180°,
∴点B、C、D、G四点共圆,
∴∠CDN=∠CBM,
如下图,过点C作CM⊥BF于点M,过点C作CN⊥ED于点N,
∴∠CDN=∠CBM=90°,
又∵CB=CD,
∴△CBM≌△CDN,
∴S四边形BCDG=S四边形CMGN=2S△CGN,
∵在Rt△CGN中,∠CGN=∠DBC=60°,∠CNG=90°
∴GN=![]() CG,CN=
CG,CN=![]() CG,
CG,
∴S△CGN=![]() CG2,
CG2,
∴S四边形BCDG=2S△CGN,=![]() CG2,即结论②是正确的;
CG2,即结论②是正确的;
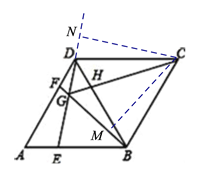
(3)∵在△ABD是等边三角形,
∴∠A=60°,∠AED>∠ABD=60°,
∴∠AED>∠A,
∴DE<AD,
同理,在△DGC中:∠GDC>∠DGC,
∴CG>CD,
∵AD=CD,
∴DE<CG,即结论③错误;
(4)如下图,过点F作FK∥AB交DE于点K,
∴△DFK∽△DAE,△GFK∽△GBE,
∴![]() ,
,![]() ,
,
∵AF=2DF,
∴![]() ,
,
∵AB=AD,AE=DF,AF=2DF,
∴BE=2AE,
∴![]() ,
,
∴BG=6FG,即结论④成立.

综上所述,本题中正确的结论是
故答案为:①②④.


科目:初中数学 来源: 题型:
【题目】如图,C为线段AD上一点,点B为CD的中点,且AD=8cm,BD=2cm.
![]()
(1)求AC的长
(2)若点E在直线AD上,且EA=3cm,求BE的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1在△ABC中,D在AB边上,DE⊥BC于E,∠A=2∠BDE.
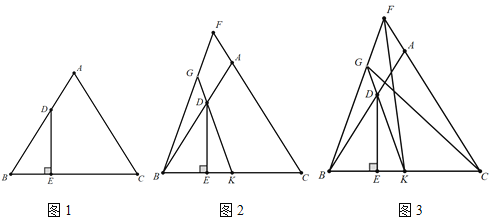
(1)求证:AB=AC;
(2)延长CA至F,连接BF,G在线段BF上,连接DG,∠F=∠BDK,延长GD交BC于K,如图2,试判断线段KG与BG的数量关系,并加以证明;
(3)在(2)的条件下,连接CG、FK,CG=FK,∠CGK=∠BFK,FG=2,CK=3,如图3,求线段BF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果把月亮绕地球旋转的轨迹看成一个圆,地心在圆心上。我们知道地球每24小时逆时针方向自转一圈(从俯视角度看),月亮每月逆时针绕地球旋转一圈.
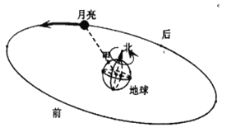
(1)求地球每小时旋转的角度;
(2)求月亮绕地球每小时旋转的角度(每月以30天记);
(3)某月15日20:00时,月亮恰好在甲地正上方(如图),到第二天大约几时几分月亮再次出现在甲地正上方?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ACB=60○,半径为2的⊙0切BC于点C,若将⊙O在CB上向右滚动,则当滚动到⊙O与CA也相切时,圆心O移动的水平距离为 ( )

A. 2π B. 4π C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC三个顶点的位置如图所示,现将△ABC平移,使点A移动到点A',点B、C的对应点分别是点B'、C'.
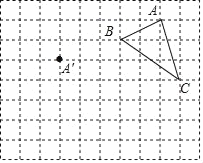
(1)△ABC的面积是 ;
(2)画出平移后的△A'B'C';
(3)若连接AA'、CC′,这两条线段的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,
, ![]() 于点
于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,下列结论:
,下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() ,
,
其中正确的有__________(只填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足学生的物质需求,我市某中学到红旗超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该红旗超市有几种进货方案?
(3)在(2)的条件下,该红旗超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学组织七、八、九年级学生参加全区作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.

(1)此次参赛的作文篇数共有 篇;
(2)扇形统计图中九年级参赛作文篇数对应的圆心角是 度,并补全条形统计图;
(3)经过评审,全校有4篇作文荣获特等奖,其中有一篇来自七年级,学校准备从特等奖作文中任选两篇刊登在校刊上,请利用画树状图或列表的方法求出七年级特等奖作文被选登在校刊上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com