
【题目】为了满足学生的物质需求,我市某中学到红旗超市准备购进甲、乙两种绿色袋装食品.其中甲、乙两种绿色袋装食品的进价和售价如下表:
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于5200元,且不超5280元,问该红旗超市有几种进货方案?
(3)在(2)的条件下,该红旗超市准备对甲种袋装食品进行优惠促销活动,决定对甲种袋装食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该红旗超市要获得最大利润应如何进货?
【答案】(1)![]() ;(2)共有17种方案;(3)当
;(2)共有17种方案;(3)当![]() 时,
时,![]() 有最大值,即此时应购进甲种绿色袋装食品240袋,表示出乙种绿色袋装食品560袋.
有最大值,即此时应购进甲种绿色袋装食品240袋,表示出乙种绿色袋装食品560袋.
【解析】
(1)根据“用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同”列出方程并解答;
(2)设购进甲种绿色袋装食品x袋,表示出乙种绿色袋装食品(800-x)袋,然后根据总利润列出一元一次不等式组解答;
(3)设总利润为W,根据总利润等于两种绿色袋装食品的利润之和列式整理,然后根据一次函数的增减性分情况讨论求解即可.
解:(1)依题意得:![]()
解得:![]() ,
,
经检验![]() 是原分式方程的解;
是原分式方程的解;
(2)设购进甲种绿色袋装食品![]() 袋,表示出乙种绿色袋装食品
袋,表示出乙种绿色袋装食品![]() 袋,根据题意得,
袋,根据题意得,
![]()
解得:![]() ,
,
∵![]() 是正整数,
是正整数,![]() ,
,
∴共有17种方案;
(3)设总利润为![]() ,则
,则![]() ,
,
①当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而增大,
的增大而增大,
所以,当![]() 时,
时,![]() 有最大值,
有最大值,
即此时应购进甲种绿色袋装食品256袋,乙种绿色袋装食品544袋;
②当![]() 时,
时,![]() ,(2)中所有方案获利都一样;
,(2)中所有方案获利都一样;
③当![]() 时,
时,![]() ,
,![]() 随
随![]() 的增大而减小,
的增大而减小,
所以,当![]() 时,
时,![]() 有最大值,
有最大值,
即此时应购进甲种绿色袋装食品240袋,表示出乙种绿色袋装食品560袋.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣30|+(b+6)2=0.点O是数轴原点.
![]()
(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
查看答案和解析>>
科目:初中数学 来源: 题型:
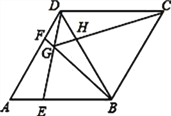
【题目】如图,在菱形ABCD中,AB=BD.点E、F分别在AB、AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.下列结论:①△AED≌△DFB; ②S四边形BCDG=![]() CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
CG2;③DE=CG;④若AF=2DF,则BG=6GF.其中正确的结论_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
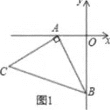
【题目】如图1,![]() ,以
,以![]() 点为顶点、
点为顶点、![]() 为腰在第三象限作等腰
为腰在第三象限作等腰![]() .
.
(1)求![]() 点的坐标;
点的坐标;
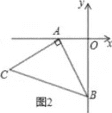
(2)如图2,在平面内是否存在一点![]() ,使得以
,使得以![]() 为顶点的四边形为平行四边形?若存在,请写出
为顶点的四边形为平行四边形?若存在,请写出![]() 点坐标;若不存在,请说明理由;
点坐标;若不存在,请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).

(1)四边形EFGH是什么四边形?证明你的结论.
(2)当四边形ABCD的对角线满足 条件时,四边形EFGH是矩形;
(3)你学过的哪种特殊四边形的中点四边形是矩形? . (填一种即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
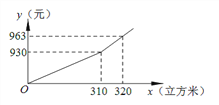
【题目】某市为鼓励市民节约用气,对居民管道天然气实行两档阶梯式收费.年用天然气量310立方米及以下为第一档;年用天然气量超出310立方米为第二档.某户应交天然气费y(元)与年用天然气量x(立方米)的关系如图所示,观察图像并回答下列问题:
(1)年用天然气量不超过310立方米时,求y关于x的函数解析式(不写定义域);
(2)小明家2017年天然气费为1029元,求小明家2017年使用天然气量.
查看答案和解析>>
科目:初中数学 来源: 题型:
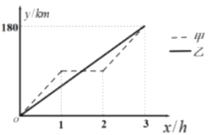
【题目】甲、乙两车间同时从A地出发前往B地,沿着相同的路线匀速驶向B地,甲车中途由于某种原因休息了1小时,然后按原速继续前往B地,两车离A地的距离y(km)与行驶的时间x(h)之间的函数关系如图所示:
(1)A、B两地的距离是__________km;
(2)求甲车休息后离A地的距离y(km)与x(h)之间的函数关系;
(3)请直接写出甲、乙两车何时相聚15km。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,边长为2的正方形![]() 中,
中,![]() 是对角线
是对角线![]() 上的一个动点(与点
上的一个动点(与点![]() 、
、![]() 不重合),过点
不重合),过点![]() 作
作![]() ,
,![]() 交射线
交射线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .
.
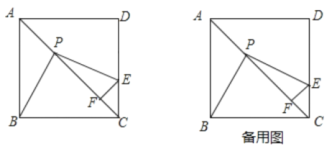
(1)求证:![]() :
:
(2)在点![]() 的运动过程中,
的运动过程中,![]() 的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
的长度是否发生变化?若不变,试求出这个不变的值,写出解答过程:若变化,试说明理由:
(3)在点![]() 的运动过程中,
的运动过程中,![]() 能否为等腰三角形?如果能,直接写出此时
能否为等腰三角形?如果能,直接写出此时![]() 的长;如果不能,试说明理由.
的长;如果不能,试说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com