
����Ŀ����ͼ���������ϵ�A��ʾ����a����B��ʾ��b��a��b����|a��30|+��b+6��2=0����O������ԭ�㣮
![]()
��1����A��ʾ����Ϊ�� ������B��ʾ����Ϊ�� �����߶�AB�ij�Ϊ�� ����
��2������A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC��������������һ��C��ʹAC=2BC�����C�������ϱ�ʾ����Ϊ�� ����
��3�����ж���P��Q����B���������P��ÿ��1����λ���ȵ��ٶ����յ�A�ƶ�������P�ƶ���O��ʱ����Q�Ŵ�B�����������ÿ��3����λ���ȵ��ٶ������ƶ����ҵ���P����A��ʱ����Q��ֹͣ�ƶ������P�ƶ���ʱ��Ϊt�룬�ʣ���tΪ����ʱ��P��Q�������4����λ���ȣ�
���𰸡���1��30����6�� 36����2��6��42����3����tΪ4�롢7���11��ʱ��P��Q��������4����λ���ȣ�
��������
��1������ż�η��Լ�����ֵ�ķǸ��Լ������a��b��ֵ���ɵõ�A��ʾ��������B��ʾ�������ٸ��������ľ��빫ʽ�����߶�AB�ij�����2���������������C���߶�AB�ϣ���C������AB�ϣ��������ۼ�����⣻��3����0��t��6��6��x��9��9��t��30����������ǣ����������ľ��빫ʽ���PQ=4���ɵó�����t��һԪһ�η��̣���֮���ɵó����ۣ�
��1����|a��30|+��b+6��2=0��
��a��30=0��b+6=0��
���a=30��b=��6��
AB=30������6��=36��
�ʵ�A��ʾ����Ϊ30����B��ʾ����Ϊ��6������AB�ij�Ϊ36��
��2����C���߶�AB�ϣ�
��AC=2BC��
��AC=36��![]() =24��
=24��
��C�������ϱ�ʾ����Ϊ30��24=6��
��C������AB�ϣ�
��AC=2BC��
��AC=36��2=72��
��C�������ϱ�ʾ����Ϊ30��72=��42��
�ʵ�C�������ϱ�ʾ����Ϊ6��42��
��3������t���P��ʾ����Ϊt��6����Q��ʾ����Ϊ![]() ��
��
��i����0��t��6ʱ����Q���ڵ�A����
��PQ=t��6������6��=t=4��
��ii����6��x��9ʱ����P�ڵ�Q���Ҳ࣬
�ࣨt��6����[3��t��6����6]=4��
��ã�t=7��
��iii����9��t��30ʱ����P�ڵ�Q����࣬
��3��t��6����6����t��6��=4��
��ã�t=11��
������������tΪ4�롢7���11��ʱ��P��Q��������4����λ���ȣ�
�ʴ�Ϊ��30����6��36��6��42��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
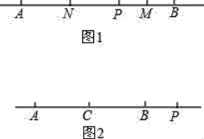
����Ŀ��(1)��ͼ1����ֱ��![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() ����֮�䣬��
����֮�䣬��![]() Ϊ�߶�PB���е㣬��
Ϊ�߶�PB���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() ����ʹ����
����ʹ����![]() �ķ���
�ķ���![]() ��.
��.
�����߶�![]() �ij���
�ij���
���߶�![]() �ij����
�ij����![]() ���߶�
���߶�![]() �ϵ�λ���й�����˵�����ɣ�
�ϵ�λ���й�����˵�����ɣ�
(2)��ͼ2����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() ���߶�
���߶�![]() ���ӳ����ϣ���˵��
���ӳ����ϣ���˵��![]() ��ֵ����.
��ֵ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ�߶�AD��һ�㣬��BΪCD���е㣬��AD=8cm��BD=2cm.
![]()
(1)��AC�ij�
(2)����E��ֱ��AD�ϣ���EA=3cm����BE�ij�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������������A��B��C����ʾ�����ֱ��ǩ�4����2��3��
![]()
��1����ʹC��B����ľ�����A��B����ľ����2�������轫��C�����ƶ��� ������λ��
��2����A��B��C��ʼ���������˶�������A��ÿ��a����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶������˶�ʱ��Ϊt�룺
����A��B��C��ʾ�����ֱ����� ������ ������ �������ú�a��t�Ĵ���ʽ��ʾ����
������B���C֮��ľ����ʾΪd1����A���B֮��ľ����ʾΪd2����aΪ��ֵʱ��5d1��3d2��ֵ��������ʱ��t�ı仯���ı䣬�����ʱ5d1��3d2��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����Ż������ķ�չ��ͬѧ�ǵ�ѧϰϰ��Ҳ���˸ı䣬һЩͬѧ��������������ʱ��ϲ���������Ҵ𰸣����������⣬ijУ�����˲���ѧ�����������������(��Ϊ���ɡ�����ν������)���������������Ƴ�ͼ1��ͼ2������������ͳ��ͼ��
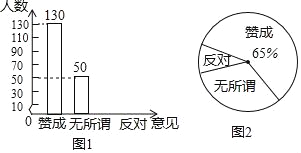
�����ͼ���ṩ����Ϣ������������⣺
(1)�˴γ��������У��������˶�����ѧ����
(2)��ͼ1����������
(3)�������ͳ��ͼ�г��������������ѧ���������ε�Բ�ĽǵĶ�����
(4)���ݳ�����������������Ƹ�У1500��ѧ�����ж�����ѧ����������ν�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���ڼ䣬�ľߵ��ϰ幺��100ֻ�����ͺŵ��ľ߽������ۣ�����ۺ��ۼ�֮��Ĺ�ϵ���±���
�ͺ� | ���ۣ�Ԫ/ֻ�� | �ۼۣ�Ԫ/ֻ�� |
A�� | 10 | 14 |
B�� | 15 | 22 |
��1���ϰ���ν�������ʹ������ǡ��Ϊ1350Ԫ��
��2��Ҫʹ�����ľ�������������500Ԫ����ô�ϰ�����ܹ���A���ľ߶���ֻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�ڡ�ABC�У�D��AB���ϣ�DE��BC��E����A=2��BDE.
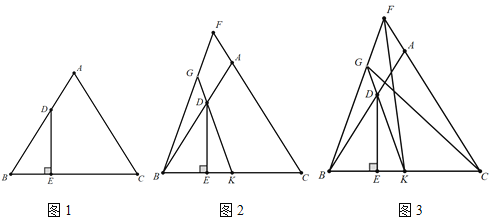
��1����֤��AB=AC��
��2���ӳ�CA��F������BF��G���߶�BF�ϣ�����DG����F=��BDK���ӳ�GD��BC��K����ͼ2�����ж��߶�KG��BG��������ϵ��������֤����
��3���ڣ�2���������£�����CG��FK��CG=FK����CGK=��BFK��FG=2,CK=3,��ͼ3�����߶�BF�ij���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������Ƶ�����ת�Ĺ켣����һ��Բ��������Բ���ϡ�����֪������ÿ24Сʱ��ʱ�뷽����תһȦ���Ӹ��ӽǶȿ���������ÿ����ʱ���Ƶ�����תһȦ.
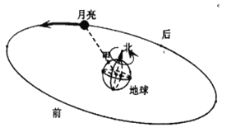
��1�������ÿСʱ��ת�ĽǶȣ�
��2���������Ƶ���ÿСʱ��ת�ĽǶȣ�ÿ����30��ǣ���
��3��ij��15��20:00ʱ������ǡ���ڼ����Ϸ�����ͼ�������ڶ����Լ��ʱ���������ٴγ����ڼ����Ϸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������ѧ����������������ij��ѧ�����쳬���������ס���������ɫ��װʳƷ.���мס���������ɫ��װʳƷ�Ľ��ۺ��ۼ����±���
�� | �� | |
���ۣ�Ԫ/���� |
|
|
�ۼۣ�Ԫ/���� | 20 | 13 |
��֪����2000Ԫ�������ִ�װʳƷ����������1600Ԫ�������ִ�װʳƷ��������ͬ.
��1����![]() ��ֵ��
��ֵ��
��2��Ҫʹ�����ļס���������ɫ��װʳƷ��800��������������=�ۼ�-���ۣ�������5200Ԫ���Ҳ���5280Ԫ���ʸú��쳬���м��ֽ���������
��3���ڣ�2���������£��ú��쳬�����Լ��ִ�װʳƷ�����Żݴ�����������Լ��ִ�װʳƷÿ���Ż�![]() Ԫ���ۣ����ִ�װʳƷ�۸�.��ô�ú��쳬��Ҫ����������Ӧ��ν�����
Ԫ���ۣ����ִ�װʳƷ�۸�.��ô�ú��쳬��Ҫ����������Ӧ��ν�����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com