
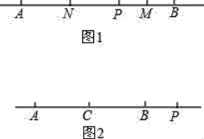
【题目】(1)如图1,在直线![]() 上,点
上,点![]() 在
在![]() 、
、![]() 两点之间,点
两点之间,点![]() 为线段PB的中点,点
为线段PB的中点,点![]() 为线段
为线段![]() 的中点,若
的中点,若![]() ,且使关于
,且使关于![]() 的方程
的方程![]() 无解.
无解.
①求线段![]() 的长;
的长;
②线段![]() 的长与点
的长与点![]() 在线段
在线段![]() 上的位置有关吗?请说明理由;
上的位置有关吗?请说明理由;
(2)如图2,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 的延长线上,试说明
的延长线上,试说明![]() 的值不变.
的值不变.
【答案】(1)①AB=4;②线段![]() 的长与点
的长与点![]() 在线段
在线段![]() 上的位置无关,理由见解析;
上的位置无关,理由见解析;
(2)见解析.
【解析】
(1)由关于![]() 的方程
的方程![]() 无解.可得
无解.可得![]() =0,从而可求得n的值;
=0,从而可求得n的值;
(2)根据线段中点的定义可知PN=![]() AP,PM=
AP,PM=![]() PB,从而得到MN=
PB,从而得到MN=![]() (PA+PB)=
(PA+PB)=![]() AB,于是可求;
AB,于是可求;
(3)设AB=a,BP=b.先表示PB+PA的长,然后再表示PC的长,最后代入计算即可.
解:(1)①∵关于![]() 的方程
的方程![]() 无解.
无解.
∴![]() =0,
=0,
解得:n=4.
故AB=4.
②线段![]() 的长与点
的长与点![]() 在线段
在线段![]() 上的位置无关,理由如下:
上的位置无关,理由如下:
∵M为线段PB的中点,
∴PM= ![]() PB.
PB.
同理:PN= ![]() AP..
AP..
∴MN=PN+PM= ![]() (PB+AP)=
(PB+AP)= ![]() AB=
AB= ![]() ×4=2.
×4=2.
∴线段MN的长与点P在线段AB上的位置无关.
(2)设AB=a,BP=b,
则PA+PB=a+b+b=a+2b.
∵C是AB的中点,
![]()
![]()
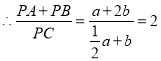 ,
,
所以![]() 的值不变.
的值不变.


科目:初中数学 来源: 题型:
【题目】如图,C、D是直线AB上两点,DE平分∠CDF,∠ACE=60°,∠CDF=60°,求∠CED的度数.请完善解答过程,并在括号内填写相应的理论依据.
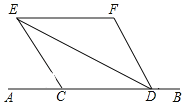
解:∵∠ACE=60°,∠CDF=60°,(已知)
∴∠ACE=∠CDF.(等量代换)
∴ ∥ ,( )
∴∠CED=∠ ,( )
∵DE平分∠CDF,(已知)
∴∠EDF=![]() ∠CDF=
∠CDF=![]() ×60°=30°.( )
×60°=30°.( )
∴∠CED=30°.(等量代换)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,观察函数y=|x|的图象,写出它的两条的性质;
(2)在图1中,画出函数y=|x-3|的图象;
根据图象判断:函数y=|x-3|的图象可以由y=|x|的图象向 平移 个单位得到;
(3)①函数y=|2x+3|的图象可以由y=|2x|的图象向 平移 单位得到;
②根据从特殊到一般的研究方法,函数y=|kx+3|(k为常数,k≠0)的图象可以由函数y=|kx|(k为常数,k≠0)的图象经过怎样的平移得到.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前,步行已成为人们最喜爱的健身方法之一,通过手机可以计算行走的步数与相应的能量消耗.对比手机数据发现:小琼步行![]() 步与小刚步行
步与小刚步行![]() 步消耗的能量相同,若每消耗
步消耗的能量相同,若每消耗![]() 千卡能量小琼行走的步数比小刚多
千卡能量小琼行走的步数比小刚多![]() 步,求小刚每消耗
步,求小刚每消耗![]() 千卡能量需要行走多少步?
千卡能量需要行走多少步?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.

(1)求∠BOD的度数;
(2)试判断OE是否平分∠BOC,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
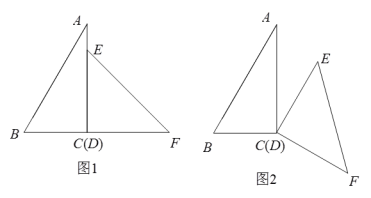
【题目】将一副直角三角板(![]() ,
,![]() )按图1方式摆放(即
)按图1方式摆放(即![]() 与
与![]() 重合、
重合、![]() 与
与![]() 共线).
共线).
(1)如图2,当![]() 绕点
绕点![]() 旋转至
旋转至![]() 时,求
时,求![]() 的度数:
的度数:
(2)若![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,回到起始位置停止,设旋转时间为t,当t为何值时,
的速度顺时针旋转,回到起始位置停止,设旋转时间为t,当t为何值时,![]() (
(![]() 与
与![]() 始终不共线);
始终不共线);
(3)若![]() 绕点
绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转的同时,
的速度顺时针旋转的同时,![]() 也绕点
也绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,当
的速度顺时针旋转,当![]() 回到起始位置时全都停止旋转.设旋转时间为t,在运动过程中,当t为何值时,
回到起始位置时全都停止旋转.设旋转时间为t,在运动过程中,当t为何值时,![]() 的边所在直线恰好平分
的边所在直线恰好平分![]() ?试直接写出t值.
?试直接写出t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
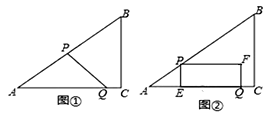
【题目】如图①,在Rt△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB﹣BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动,点Q从点C出发,沿CA方向以每秒![]() 个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
个单位长度的速度运动,P,Q两点同时出发,当点P停止时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长;(用含t的代数式表示)
(2)连结PQ,当PQ与△ABC的一边平行时,求t的值;
(3)如图②,过点P作PE⊥AC于点E,以PE,EQ为邻边作矩形PEQF.设矩形PEQF与△ABC重叠部分图形的面积为S.直接写出点P在运动过程中S与t之间的函数关系式和自变量的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上点A表示的数a、点B表示数b,a、b满足|a﹣30|+(b+6)2=0.点O是数轴原点.
![]()
(1)点A表示的数为 ,点B表示的数为 ,线段AB的长为 .
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=2BC,则点C在数轴上表示的数为 .
(3)现有动点P、Q都从B点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到O点时,点Q才从B点出发,并以每秒3个单位长度的速度向右移动,且当点P到达A点时,点Q就停止移动,设点P移动的时间为t秒,问:当t为多少时,P、Q两点相距4个单位长度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com