
����Ŀ����1����ͼ1���۲캯��y=|x|��ͼ��д���������������ʣ�
��2����ͼ1�У���������y=|x-3|��ͼ��
����ͼ���жϣ�����y=|x-3|��ͼ�������y=|x|��ͼ���� ƽ�� ����λ�õ���
��3���ٺ���y=|2x+3|��ͼ�������y=|2x|��ͼ���� ƽ�� ��λ�õ���
�ڸ��ݴ����һ����о�����������y=|kx+3|��kΪ������k��0����ͼ������ɺ���y=|kx|��kΪ������k��0����ͼ��������ƽ�Ƶõ���

���𰸡���1���𰸼���������2����ͼ���������ң�3����3������![]() �ڴ𰸼�����.
�ڴ𰸼�����.
��������
��1�����ݺ�����ͼ��õ����������ʼ��ɣ�
��2����������y=|x-3|��ͼ����ݺ���y=|x-3|��ͼ�ɵõ����ۣ�
��3���ٸ��ݣ�2���Ľ��ۼ��ɵõ������
�ڵ�k��0ʱ��k��0ʱ�����������ƽ��![]() ����λ���ȣ�
����λ���ȣ�
�⣺��1��������y=|x|��ͼ�����y��Գƣ�����x��0ʱ��y��x���������С����x��0ʱ��y��x�����������
��2������y=|x-3|��ͼ����ͼ��ʾ��

����y=|x-3|��ͼ�������y=|x|��ͼ������ƽ��3����λ�õ���
��3��������y=|2x+3|��ͼ�������y=|2x|��ͼ������ƽ��![]() ��λ�õ���
��λ�õ���
����k��0ʱ������ƽ��![]() ����λ���ȣ�
����λ���ȣ�
��k��0ʱ������ƽ��![]() ����λ����.
�������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ�������1��3��5��7������2015����һ�����ɣ���ͼ��ʽ�����г�һ������
��1����������У����ж��ٸ�����2011�ڵڼ��еڼ��У�����57�ڵ�4�е�5�У���
��2����ͼ����һʮ�ֿ��ڱ��������ס5���������м����Ϊa���ô���ʽ��ʾʮ�ֿ��е������֮�ͣ�
��3��ʮ�ֿ��е�������ĺ��ܵ���6075�����ܣ���д����������������ܣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�ı߳�Ϊ4����P��AB���ϵ�һ�����㣬����CP������P��PC�Ĵ��߽�AD�ڵ�E���� PEΪ����������PEFG������G���߶�PC�ϣ��Խ���EG��PF�ཻ�ڵ�O��
��1����AP=1����AE= ��
��2������֤����Oһ���ڡ�APE�����Բ�ϣ�
�ڵ���P�ӵ�A�˶�����Bʱ����OҲ��֮�˶������O������·������
��3���ڵ�P�ӵ�A����B���˶������У���APE�����Բ��Բ��Ҳ��֮�˶������Բ�ĵ�AB�ߵľ�������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y��kx+b��k��0����ͼ����x�ύ�ڵ�A����y�ύ�ڵ�B��0��2������������������y��![]() x��ͼ���ڵ�C��m��3����
x��ͼ���ڵ�C��m��3����
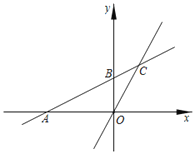
(1)��һ�κ���y��kx+b��k��0���ĺ�����ϵʽ��
(2)��AOC�����Ϊ______��
(3)����M�ڵڶ����ޣ���MAB����ABΪֱ�DZߵĵ���ֱ�������Σ�ֱ��д����M�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������������У�ÿ��С�����εı߳���Ϊ1��ÿ��С�����εĶ���и�㣮
��1����ͼ���У��߶�AB�ij���Ϊ ������ͼ�л�����CΪֱ�Ƕ����Rt��ABC��ʹ��C�ڸ���ϣ�����ͼ�л������е�C��
��2����ͼ���У��Ը��Ϊ���㣬�������̶ȵ�ֱ��������ABCD��ʹ�������Ϊ13���ٻ�һ��ֱ��PQ�����������ζԽ����غϣ���ʹPQǡ�ý�������ABCD��������ȷ֣�������ͼ�ۼ�����
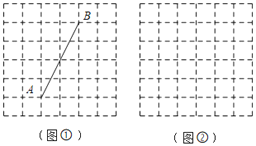
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����һ�������Թ�����2���Թ��ĵ�һ���սǣ�3�ڵ�2���սǣ�5�ڵ�3���սǣ�7�ڵ�4���սǣ�����ô��101���ս���_____��
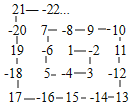
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB=��DOC=90����OEƽ�֡�AOD�������ӳ�����OE��F.
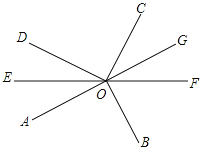
��1����AOD�͡�BOC�Ƿ���˵�����ɣ�
��2������OF�ǡ�BOC��ƽ������˵�����ɣ�
��3�������ӳ�����OA����G������OG����COF�ֳ���4��3�������ǣ����AOD.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
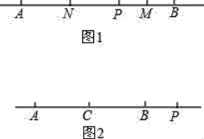
����Ŀ��(1)��ͼ1����ֱ��![]() �ϣ���
�ϣ���![]() ��
��![]() ��
��![]() ����֮�䣬��
����֮�䣬��![]() Ϊ�߶�PB���е㣬��
Ϊ�߶�PB���е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() ����ʹ����
����ʹ����![]() �ķ���
�ķ���![]() ��.
��.
�����߶�![]() �ij���
�ij���
���߶�![]() �ij����
�ij����![]() ���߶�
���߶�![]() �ϵ�λ���й�����˵�����ɣ�
�ϵ�λ���й�����˵�����ɣ�
(2)��ͼ2����![]() Ϊ�߶�
Ϊ�߶�![]() ���е㣬��
���е㣬��![]() ���߶�
���߶�![]() ���ӳ����ϣ���˵��
���ӳ����ϣ���˵��![]() ��ֵ����.
��ֵ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��CΪ�߶�AD��һ�㣬��BΪCD���е㣬��AD=8cm��BD=2cm.
![]()
(1)��AC�ij�
(2)����E��ֱ��AD�ϣ���EA=3cm����BE�ij�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com