
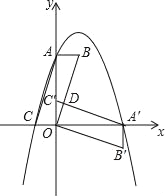
【题目】如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=﹣x2+2x+3经过点A、C、A′三点.
(1)求A、A′、C三点的坐标;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;
(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M的坐标.
【答案】(1)C(﹣1,0),A′(3,0),A(0,3);(2)![]() ;(3)S△AMA′==﹣
;(3)S△AMA′==﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,∴当m=
,∴当m=![]() 时,S△AMA'的值最大,最大值为
时,S△AMA'的值最大,最大值为![]() ,此时M点坐标为(
,此时M点坐标为(![]() ,
,![]() ).
).
【解析】
(1)利用抛物线与x轴的交点问题可求出C(﹣1,0),A′(3,0);计算自变量为0时的函数值可得到A(0,3);
(2)先由平行四边形的性质得AB∥OC,AB=OC,易得B(1,3),根据勾股定理和三角形面积公式得到OB=![]() ,S△AOB=
,S△AOB=![]() ,再根据旋转的性质得∠ACO=∠OC′D,OC′=OC=1,接着证明△C′OD∽△BOA,利用相似三角形的性质得
,再根据旋转的性质得∠ACO=∠OC′D,OC′=OC=1,接着证明△C′OD∽△BOA,利用相似三角形的性质得![]() =(
=(![]() )2,则可计算出S△C′OD;
)2,则可计算出S△C′OD;
(3)根据二次函数图象上点的坐标特征,设M点的坐标为(m,﹣m2+2m+3),0<m<3,作MN∥y轴交直线AA′于N,求出直线AA′的解析式为y=﹣x+3,则N(m,﹣m+3),于是可计算出MN=﹣m2+3m,再利用S△AMA′=S△ANM+S△MNA′和三角形面积公式得到S△AMA′=﹣![]() m2+
m2+![]() m,然后根据二次函数的最值问题求出△AMA′的面积最大值,同时即可确定此时M点的坐标.
m,然后根据二次函数的最值问题求出△AMA′的面积最大值,同时即可确定此时M点的坐标.
(1)当y=0时,﹣x2+2x+3=0,
解得x1=3,x2=﹣1,
则C(﹣1,0),A′(3,0),
当x=0时,y=3,则A(0,3);
(2)∵四边形ABOC为平行四边形,
∴AB∥OC,AB=OC,
而C(﹣1,0),A(0,3),
∴B(1,3),
∴OB=![]() =
=![]() ,S△AOB=
,S△AOB=![]() ×3×1=
×3×1=![]() ,
,
又∵平行四边形ABOC旋转90°得平行四边形A′B′OC′,
∴∠ACO=∠OC′D,OC′=OC=1,
又∵∠ACO=∠ABO,
∴∠ABO=∠OC′D.
又∵∠C′OD=∠AOB,
∴△C′OD∽△BOA,
∴![]() =(
=(![]() )2=(
)2=(![]() )2=
)2=![]() ,
,
∴S△C′OD=![]() ×
×![]() =
=![]() ;
;
(3)设M点的坐标为(m,﹣m2+2m+3),0<m<3,
作MN∥y轴交直线AA′于N,易得直线AA′的解析式为y=﹣x+3,则N(m,﹣m+3),
∵MN=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,
∴S△AMA′=S△ANM+S△MNA′
=![]() MN3
MN3
=![]() (﹣m2+3m)
(﹣m2+3m)
=﹣![]() m2+
m2+![]() m
m
=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
∴当m=![]() 时,S△AMA'的值最大,最大值为
时,S△AMA'的值最大,最大值为![]() ,此时M点坐标为(
,此时M点坐标为(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
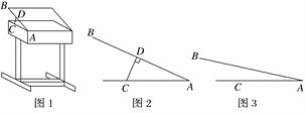
【题目】某课桌生产厂家研究发现,倾斜12°~24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30 cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长;
(2)如图3,当∠BAC=12°时,求AD的长.(结果保留根号)
(参考数据:sin 24°≈0.40,cos 24°≈0.91,tan 24°≈0.46,sin 12°≈0.20)
查看答案和解析>>
科目:初中数学 来源: 题型:
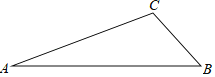
【题目】如图,在△ABC纸板中,AC=4,BC=2,AB=5,P是AC上一点,过点P沿直线剪下一个与△ABC相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结果如此巧合!
下面是小颖对一道题目的解答.
题目:如图,Rt△ABC的内切圆与斜边AB相切于点D,AD=3,BD=4,求△ABC的面积.
解:设△ABC的内切圆分别与AC、BC相切于点E、F,CE的长为x.
根据切线长定理,得AE=AD=3,BF=BD=4,CF=CE=x.
根据勾股定理,得(x+3)2+(x+4)2=(3+4)2.
整理,得x2+7x=12.
所以S△ABC=![]() ACBC
ACBC
=![]() (x+3)(x+4)
(x+3)(x+4)
=![]() (x2+7x+12)
(x2+7x+12)
=![]() ×(12+12)
×(12+12)
=12.
小颖发现12恰好就是3×4,即△ABC的面积等于AD与BD的积.这仅仅是巧合吗?
请你帮她完成下面的探索.
已知:△ABC的内切圆与AB相切于点D,AD=m,BD=n.
可以一般化吗?
(1)若∠C=90°,求证:△ABC的面积等于mn.
倒过来思考呢?
(2)若ACBC=2mn,求证∠C=90°.
改变一下条件……
(3)若∠C=60°,用m、n表示△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
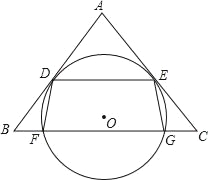
【题目】如图,O是△ABC内一点,⊙O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC.连接 DF、EG.
(1)求证:AB=AC.
(2)已知 AB=5,BC=6.求四边形DFGE是矩形时⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点 O 是△ABC 的边 AB 上一点,以 OB 为半径的⊙O 交 BC 于点 D,过点 D 的切线交 AC 于点 E,且 DE⊥AC.
(1)证明:AB=AC;
(2)设 AB=![]() cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.
cm,BC=2cm,当点 O 在 AB 上移动到使⊙O 与边 AC 所在直线相切时, 求⊙O 的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径长是( )

A. 2cm B. 2.5cm C. 3cm D. 4cm
查看答案和解析>>
科目:初中数学 来源: 题型:
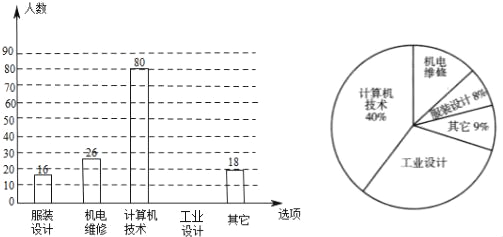
【题目】每年5月的第二周为“职业教育活动周”,今年我省开展了以“弘扬工匠精神,打造技能强国”为主题的系列活动.活动期间某职业中学组织全校师生并邀请学生家长和社区居民参加“职教体验观摩”活动,相关职业技术人员进行了现场演示,活动后该校教务处随机抽取了部分学生进行调查:“你最感兴趣的一种职业技能是什么?”并对此进行了统计,绘制了统计图(均不完整).请解答以下问题:
(1)补全条形统计图和扇形统计图;
(2)若该校共有1800名学生,请估计该校对“工业设计”最感兴趣的学生有多少人?
(3)要从这些被调查的学生中,随机抽取一人进行访谈,那么正好抽到对“机电维修”最感兴趣的学生的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com