
����Ŀ��(1)����ͼ�еĸ�����������겻�䣬�����궼�˩�1����ԭͼ����ȣ�����ͼ����ʲô�仯���뻭��ͼ�β�д�����ۣ�
(2)����ͼ�еĸ�����ĺ����겻�䣬�����궼����-1����ԭͼ����ȣ�����ͼ����ʲô�仯���뻭��ͼ�β�д�����ۣ�
(3)����ͼ�еĸ�����ĺ����겻�䣬�����궼+3����ԭͼ����ȣ�����ͼ����ʲô�仯���뻭��ͼ�β�д�����ۣ�
(4)����ͼ�еĸ�����ĺ����ꩁ2�������겻�䣬��ԭͼ����ȣ�����ͼ����ʲô�仯���뻭��ͼ�β�д�����ۣ�
(5)����ͼ�еĸ�����ĺ����궼��2�������궼��2����ԭͼ����ȣ�����ͼ����ʲô�仯���뻭��ͼ�β�д�����ۣ�
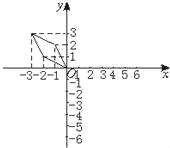
���𰸡�(1)��ͼ������������ͼ����ԭͼ�ι���y��Գƣ�(2)��ͼ������������ͼ����ԭͼ�ι���x��Գ�(3)��ͼ����������ԭͼ�Ĺ�ϵ������ƽ��3����λ��(4)��ͼ����������ԭͼ�Ĺ�ϵ������ƽ��2����λ��(5)��ͼ������������ͼ����ԭͼ�Ĺ�ϵ�ǷŴ�Ϊԭ����2����
��������
��1���ȶ���ͼ�и�������꣬���ú��������-1�ó������꣬����������������㣬˳�����ӣ��ó���ԭͼ�Ĺ�ϵ��
��2��������ĺ����겻�䣬�����궼����-1�ó������꣬����������������㣬˳�����ӣ��ó���ԭͼ�Ĺ�ϵ��
��3��������ĺ����겻�䣬�����궼+3�ó������꣬����������������㣬˳�����ӣ��ó���ԭͼ�Ĺ�ϵ��
��4��������ĺ�����-2�������겻��ó������꣬����������������㣬˳�����ӣ��ó���ԭͼ�Ĺ�ϵ��
��5��������ĺ����궼����2�������궼����2���ó������꣬����������������㣬˳�����ӣ��ó���ԭͼ�Ĺ�ϵ��
�⣺(1)��ͼ�϶������������ֱ���(0��0)(��1��2)(��3��3)(��2��1)
������������겻�䣬�����궼���ԩ�1��
(0��0)(1��2)(3��3)(2��1)
������������������ͼ����
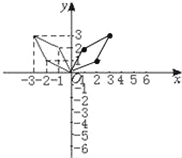
��ͼ�п��Եó�����ͼ����ԭͼ�ι���y��Գƣ�
(2)�������겻�䣬��������ԩ�1�õ��µ����꣺
(0��0)(��1����2)(��3����3)(��2����1)
��ͼ�������������ͼ
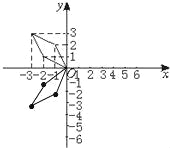
�ó�����ͼ����ԭͼ�ι���x��Գƣ�
(3)������ĺ����겻�䣬�����궼+3�õ��µ����꣺
(0��3)(��1��5)(��3��6)(��2��4)
������ϵ����������ͼ����
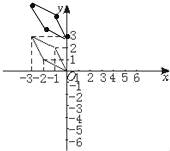
�ó���ԭͼ�Ĺ�ϵ������ƽ��3����λ��
(4)������ĺ����ꩁ2�������겻��ó������꣺
(��2��0)(��3��2)(��5��3)(��4��1)
������ϵ��������㣬˳�����ӵ�ͼ���£�
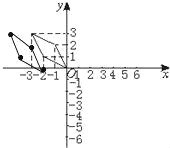
�ó���ԭͼ�Ĺ�ϵ������ƽ��2����λ��
(5)������ĺ����궼����2�������궼����2���ó������꣺
(0��0)(��2��4)(��6��6)(��4��2)
������ϵ�������������겢˳������ͼ���£�
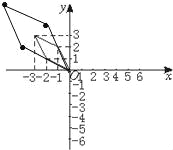
�ó���ԭͼ�Ĺ�ϵ�ǷŴ�Ϊԭ����2����
�ʴ�Ϊ��(1)��ͼ������������ͼ����ԭͼ�ι���y��Գƣ�(2)��ͼ������������ͼ����ԭͼ�ι���x��Գ�(3)��ͼ����������ԭͼ�Ĺ�ϵ������ƽ��3����λ��(4)��ͼ����������ԭͼ�Ĺ�ϵ������ƽ��2����λ��(5)��ͼ������������ͼ����ԭͼ�Ĺ�ϵ�ǷŴ�Ϊԭ����2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
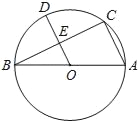
����Ŀ����ͼ��AB�ǡ�O��ֱ������C�ǡ�O��һ�㣬����BC��AC��OD��BC��E��
��1����֤��OD��AC��
��2����BC��8��DE��3�����O��ֱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
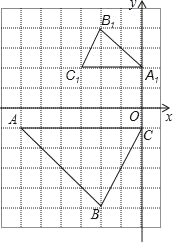
����Ŀ����ͼ����ABC����A1B1C1��λ��ͼ�Σ�
��1���������Ͻ���ƽ��ֱ������ϵ��ʹ�õ�A������Ϊ����6����1������C1������Ϊ����3��2�������B������Ϊ�� ����
��2���Ե�AΪλ�����ģ�������ͼ������AB2C2��ʹ��AB2C2����ABCλ�ƣ���λ�Ʊ�Ϊ1��2��
��3����ͼ�ϱ����ABC����A1B1C1��λ������P����д����P������Ϊ�� ���������ı���ABCP���ܳ�Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
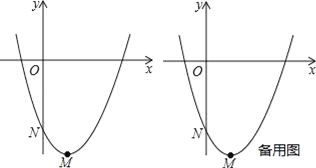
����Ŀ����֪������l��y=ax2+bx+c��a��b��c����Ϊ0���Ķ���ΪM����y��Ľ���ΪN�����dz���NΪ���㣬�Գ�����y���ҹ���M��������Ϊ������l�����������ߣ�ֱ��MNΪ������l������ֱ�ߣ�
��1����ͼ��������y=x2��2x��3�����������ߵĽ���ʽ���� ��������ֱ�ߵĽ���ʽ���� ����
��2����һ�������ߵ����������ߺ�����ֱ�߷ֱ���y=��2x2+1��y=��2x+1�������������ߵĽ���ʽ��
��3����ͼ���裨1���е�������y=x2��2x��3�Ķ���ΪM����y�ύ��ΪN������������ֱ��MN���Ƶ�N��ת����x��ƽ�У�����y������ƽ��1����λ��ֱ��n��P��ֱ��n�ϵĶ��㣬�Ƿ���ڵ�P��ʹ��POMΪֱ�������Σ������ڣ�������е�P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
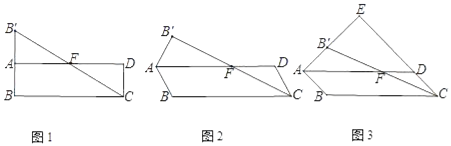
����Ŀ����ABCD�У���B����AD�ĶԳƵ�ΪB��������AB����CB����CB����AD��F�㣮
��1����ͼ1����ABC=90������֤��FΪCB�����е㣻
��2��С��ͨ���۲졢ʵ�顢������룺��ͼ2���ڵ�B�Ƶ�A��ת�Ĺ����У���Fʼ��ΪCB�����е㣮С������������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1������B����B��G��CD��AD��G�㣬ֻ��֤������ȫ�ȣ�
�뷨2������BB����AD��H�㣬ֻ��֤HΪBB�����е㣻
�뷨3������BB����BF��ֻ��֤��B��BC=90����
��
����ο�������뷨��֤��FΪCB�����е㣮��һ�ַ������ɣ�
��3����ͼ3������ABC=135��ʱ��AB����CD���ӳ����ཻ�ڵ�E����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�γ�����Ϊ���˽�ѧ���Կ����3D��ӡ��ľ�������������˺͵��Ա�����ſγ̵�ϲ���̶ȣ���������˲���ѧ����ÿ��ֻ��ѡһ����ϲ���Ŀγ�.ͼ�������ſγ���ϲ������������ͳ��ͼ��ͼ�������ſγ��С�Ů����ϲ������������ͳ��ͼ.
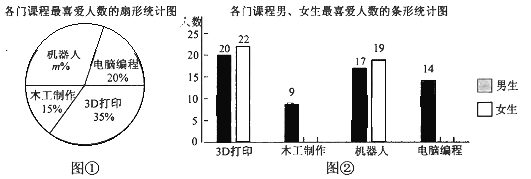
(1)��ͼ����![]() ��ֵ����ȫͼ���е�����ͳ��ͼ��������Ӧ������;
��ֵ����ȫͼ���е�����ͳ��ͼ��������Ӧ������;
(2)����У����1800��ѧ�������У��ϲ��3D��ӡ�γ̵�ѧ��Լ�ж�����?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
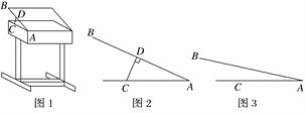
����Ŀ��ij�������������о����֣���б12����24��������������ѧ������������Ȼ���ƣ�������һ�о������Ҿ�����ˮƽ�������ɿɵ��ڽǶȵ����森����������ͼ��ͼ1��AB���Ƶ�A��ת���ڵ�C����װһ������ת��֧�ű�CD��AC��30 cm.
(1)��ͼ2������BAC��24��ʱ��CD��AB����֧�ű�CD�ij���
(2)��ͼ3������BAC��12��ʱ����AD�ij���(�����������)
(�ο����ݣ�sin 24���0.40��cos 24���0.91��tan 24���0.46��sin 12���0.20)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�β�����У�ͬѧ��Ҫ����ij������ͷA�������������ͤ��B֮��ľ��룬��ͼ����ѡ��������ͷA��ͤ��B��ͬһˮƽ���ϵĵ�P�ڵ�P�������ͷAλ�ڵ�P��ƫ������30������ͤ��Bλ�ڵ�P��ƫ��43�������ֲ��P����ͷA֮��ľ���Ϊ200�ף��������������������A��B�ľ��룮
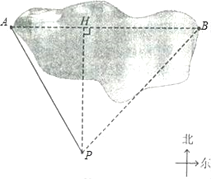
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���m x2-(m+2)x+2=0��m��0��.
��1����֤������mΪ��ֵʱ�����������������ʵ������
��2�������̵�����ʵ����������������������m��ֵ.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com