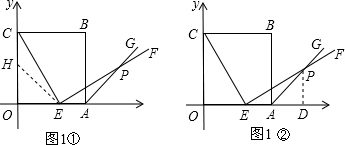
(1)证明:方法一:如图1①,在OC上截取OH=OE,则△OEH是等腰直角三角形,
∠CHE=180°-45°=135°,
∵CH=OC-OH=6-3=3,EA=OA-OE=6-3=3,
∴CH=EA,
∵AG是正方形外角平分线,
∴∠EAP=90°+45°=135°,
∴∠CHE=∠EAP=135°,
∵EF⊥CE,
∴∠CEO+∠PED=180°-90°=90°,
又∵∠ECO+∠CEO=90°,
∴∠ECO=∠PED,
在△CHE和△EAP中,

,
∴△CHE≌△EAP(ASA),
∴CE=EP;
方法二:如图1②,过点P作PD⊥x轴于点D,
∵AG是正方形外角平分线,
∴△ADP是等腰直角三角形,
设PD=x,则AD=x,
∵点E坐标为(3,0),正方形的边长为6,
∴AE=6-3=3,
∴ED=3+x,
∵EF⊥CE,
∴∠CEO+∠PED=180°-90°=90°,
又∵∠ECO+∠CEO=90°,
∴∠ECO=∠PED,
又∠COE=∠PDE=90°,
∴△CEO∽△EPD,
∴
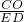
=
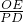
,
即
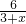
=

,
解得x=3,
∴PD=OE=3,ED=OC=6,
故,根据勾股定理可得CE=EP;
(2)解:CE=EP仍然成立.
理由如下:
方法一:同(1)可求∠CHE=∠EAP=135°,∠ECO=∠PED,
又∵CH=OC-OH=6-t,EA=OA-OE=6-t,
∴CH=EA,
在△CHE和△EAP中,

,
∴△CHE≌△EAP(ASA),
∴CE=EP;
方法二:当点E的坐标为(t,0)时,与(1)同理,
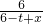
=
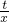
,
整理得,t
2-tx+6x-6t=0,
即(t-x)(t-6)=0,
∵点E是OA边上的点(不与点A重合),
∴t≠6,
∴t-x=0,
解得x=t,
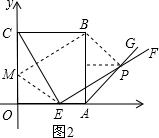
∴PD=OE=t,ED=6-t+t=6=OC,
根据勾股定理可得CE=EP;
(3)解:如图2,∵点E(t,0),
∴PE
2=CE
2=CO
2+OE
2=36+t
2,
PB
2=t
2+(6-t)
2,
设点M的坐标为(0,y),
则ME
2=t
2+y
2,BM
2=6
2+(6-y)
2,
∵四边形BMEP是平行四边形,
∴PE
2=BM
2,
即36+t
2=6
2+(6-y)
2,
解得y
1=6-t,y
2=6+t,
当y
1=6-t时,ME
2=t
2+y
2=t
2+(6-t)
2=PB
2,
∴ME=PB,
∴当点M(0,6-t)时,四边形BMEP是平行四边形,
当y
2=6+t时,ME
2=t
2+y
2=t
2+(6+t)
2≠PB
2,
∴ME≠PB,
∴当点M(0,6+t)时,四边形BMEP不是平行四边形,
综上所述,y轴上存在点M(0,6-t)时,四边形BMEP是平行四边形.
分析:(1)方法一:在OC上截取OH=OE,可得△OEH是等腰直角三角形,然后求出∠CHE=135°,且CH=EA,再根据AG是正方形外角平分线可以求出∠EAP=135°,从而得到∠CHE=∠EAP,再根据EF⊥CE推出∠ECO=∠PED,然后利用“角边角”证明△CHE和△EAP全等,根据全等三角形对应边相等即可得证;
方法二:过点P作PD⊥x轴于点D,根据AG是正方形外角平分线可得△ADP是等腰直角三角形,设PD=x,用x表示出ED,再根据EF⊥CE推出∠ECO=∠PED,从而得到△CEO和△EPD相似,根据相似三角形对应边成比例列式求出x的值,即可得证;
(2)方法一:与(1)求法相同;
方法二:与(1)同理求出PD的长度,即可得解;
(3)设点M的坐标为(0,y),根据点的坐标利用勾股定理分别表示出BM、ME、PE、PB的平方,再根据平行四边形的对边相等利用一组对边列出方程求解,用t表示出y,然后代入另一组进行验证,相等则能使四边形BMEP是平行四边形,否则不能使四边形BMEP是平行四边形.
点评:本题综合考查了一次函数,正方形的性质,相似三角形的判定与性质,等腰直角三角形的判定与性质,平行四边形的对边相等,(3)根据平行四边形的对边相等列出方程有技巧,要掌握.

 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P. ,
,
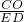 =
=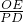 ,
,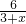 =
= ,
, ,
,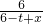 =
=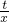 ,
,


 如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.
如图,边长为6的正方OABC的顶点O在坐标原点处,点A、C分别在x轴、y轴的正半轴上,点E是OA边上的点(不与点A重合),EF⊥CE,且与正方形外角平分线AC交于点P.