练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．下列图形中，∠1与∠2是内错角的是（　　）
    A．B．C．D．

    分析 根据内错角的定义找出即可．

    解答 解：A、是同位角，故此选项错误；
    B、是内错角，故此选项正确；
    C、是同位角，故此选项错误；
    D、不是内错角，故此选项错误；
    故选：B．

    点评 本题考查了同位角、内错角、同旁内角，熟记内错角的定义是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

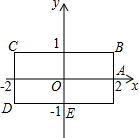    8．如图，矩形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙由点（2，0）同时出发，沿矩形BCDE的边作环绕运动，物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2016次相遇地点的坐标是（　　）
    A．（-1，-1）B．（2，0）C．（-1，1）D．（1，-1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

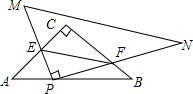    9．如图，在等腰直角三角形ABC中，AC=BC=3$\sqrt{2}$，∠C=90°，Rt△PMN的直角顶点P在线段AB上，PM、PN分别交于AC、BC于点E、F，PA：PB=1：2，∠BPF=15°，则EF的长为$\frac{2\sqrt{30}}{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．某地区有36所中学，其中九年级学生共7000名．为了了解该地区九年级学生的体重情况，请你运用所学的统计知识，将解决上述问题所要经历的几个主要步骤进行排序．①抽样调查；②设计调查问卷；③用样本估计总体；④整理数据；⑤分析数据．排序：②①④⑤③（只写序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．若最简二次根式$\sqrt{{b}^{2}+2b+2}$与$\sqrt{3+2b}$是同类根式，则b的值是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

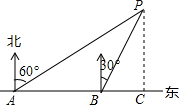    3．如图，小聪同学在东西走向的文一路A处，测得一处公共自行车租用服务点P在北偏东60°方向上，在A处往东90米的B处，又测得该服务点P在北偏东30°方向上，则该服务点P到文一路的距离PC为45$\sqrt{3}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

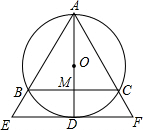    10．如图，⊙O是△ABC的外接圆，AD是⊙O的直径，AD与BC相交于点M，且BM=MC，过点D作BC的平行线，分别与AB、AC的延长线相交于点E、F．
    （1）求证：EF与⊙O相切；
    （2）若BC=2$\sqrt{15}$，MD=$\sqrt{5}$，求CE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

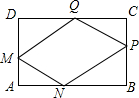    7．在一块矩形ABCD的空地上划一块平行四边形MNPQ进行绿化．如图，平行四边形MNPQ的顶点在矩形的边长，且AM=CP=xm，∠ANM=∠CQP=30°．已知矩形的边BC=100m，边AB=am，a为大于100的常数，设四边形MNPQ的面积为Sm2．
    （1）求S关于x的函数关系式，并直接写出自变量x的取值范围；
    （2）若a=200$\sqrt{3}$，求S的最大值，并求出此时x的值；
    （3）若a=400$\sqrt{3}$，请直接写出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．【问题情境】
    张老师给爱好学习的小军和小俊提出这样的一个问题：如图1，在△ABC中，AB=AC，点P为边BC上任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F，求证：PD+PE=CF．

    小军的证明思路是：如图2，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．
    小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．
    【变式探究】
    如图3，当点P在BC延长线上时，其余条件不变，求证：PD-PE=CF；
    请运用上述解答中所积累的经验和方法完成下列两题：
    【结论运用】
    如图4，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点C′处，点P为折痕EF上的任一点，过点P作PG⊥BE、PH⊥BC，垂足分别为G、H，若AD=8，CF=3，求PG+PH的值；
    【迁移拓展】
    图5是一个航模的截面示意图．在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D、C，且AD•CE=DE•BC，AB=2$\sqrt{13}$dm，AD=3dm，BD=$\sqrt{37}$dm．M、N分别为AE、BE的中点，连接DM、CN，求△DEM与△CEN的周长之和．

    查看答案和解析>>

    同步练习册答案