
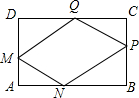
 在一块矩形ABCD的空地上划一块平行四边形MNPQ进行绿化.如图,平行四边形MNPQ的顶点在矩形的边长,且AM=CP=xm,∠ANM=∠CQP=30°.已知矩形的边BC=100m,边AB=am,a为大于100的常数,设四边形MNPQ的面积为Sm2.
在一块矩形ABCD的空地上划一块平行四边形MNPQ进行绿化.如图,平行四边形MNPQ的顶点在矩形的边长,且AM=CP=xm,∠ANM=∠CQP=30°.已知矩形的边BC=100m,边AB=am,a为大于100的常数,设四边形MNPQ的面积为Sm2.分析 (1)根据题意表示出AN、DM、DQ的长,由平行四边形面积=矩形面积-四个直角三角形面积列出函数关系式;
(2)将a=200$\sqrt{3}$代入(1)中函数解析式,配方成二次函数的顶点式,根据函数性质可得最大值;
(3)将a=400$\sqrt{3}$代入(1)中函数解析式,配方成二次函数的顶点式,根据自变量的取值范围可得其最大值.
解答 解:(1)根据题意知,AN=CQ=$\sqrt{3}$x米,DM=BP=100-x米,DQ=BN=a-$\sqrt{3}$x米,
∴S=100a-2[$\frac{1}{2}$×x$•\sqrt{3}$x+$\frac{1}{2}$•(100-x)$•(a-\sqrt{3}x)$]=-2$\sqrt{3}$x2+(100$\sqrt{3}$+a)x,(0<x<100);
(2)当a=200$\sqrt{3}$时,S=-2$\sqrt{3}$x2+300$\sqrt{3}$x=-2$\sqrt{3}$(x-75)2+11250,
∴当x=75m时,S取得最大值,最大值为11250m2;
(3)当a=400$\sqrt{3}$时,S=-2$\sqrt{3}$x2+500$\sqrt{3}$x=-2$\sqrt{3}$(x-125)2+31250$\sqrt{3}$,
∵当x<125时,S随x的增大而增大,
∴当x=100m时,S取得最大值,最大值为30000$\sqrt{3}$m2.
点评 本题主要考查二次函数的实际应用能力,根据矩形和平行四边形的性质得出所需线段的长是解题的前提,依据相等关系列出函数关系式并由函数性质确定其最大值是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com