解:(1)当a=2时,令x=0,则y=a
2=4,
∴点M(0,4),
∵y=x
2-2ax+a
2=(x-a)
2,
∴当a=2时,顶点G(2,0),
∴OM=4,OG=2,
S
△GOM=

OM•OG=

×4×2=4;
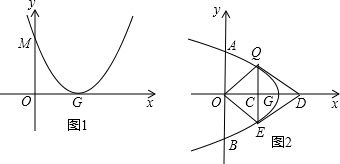
(2)①∵四边形OQDE为平行四边形,
∴OC=CE=

QE,
又∵AQ=2QC,
∴AQ=EQ,
∵QO平分∠AQC,
∴∠AQO=∠EQO,
∵在△AQO和△EQO中,
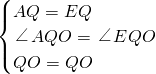
,
∴△AQO≌△EQO(SAS);
②∵由题意知G(a,0),
∴OG=a,
∵QD=OG,
∴QD=a,
∵四边形OQDE为平行四边形,
∴OE=QD=a,
又∵△AOQ≌△EOQ,
∴OA=OE=a,
即A(0,a),
由旋转知,旋转前抛物线点A的坐标为(2a,a),
把(2a,a)代入y=x
2-2ax+a
2得,4a
2-2a•a+a
2=a,
即a
2=a,
解得a=1或0,
∵a为常数,a>0
∴a=0不合题意,舍去,
∴a=1.
分析:(1)先求出点M的坐标,再把抛物线解析式整理成顶点式形式,然后求出点G的坐标,从而得到OM、OG,然后根据三角形的面积公式列式计算即可得解;
(2)①根据平行四边形的对角线互相平分可得OC=CE=

QE,然后求出AQ=EQ,再根据角平分线的定义可得∠AQO=∠EQO,然后利用“边角边”证明△AQO和△EQO全等;
②根据平行四边形的对边相等可得OE=QD,再根据全等三角形对应边相等可得OA=OE,从而得到点A的坐标,再根据旋转的性质求出点A旋转前的坐标,然后代入抛物线解析式进行计算即可求出a的值.
点评:本题是二次函数综合题型,主要考查了二次函数与y轴的交点的求解,顶点坐标,全等三角形的判定与性质,平行四边形的对边相等,以及旋转的性质,(2)中求出点A的坐标以及旋转前的坐标是解题的关键,也是本题的难点.

 OM•OG=
OM•OG= ×4×2=4;
×4×2=4; QE,
QE,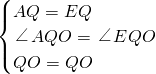 ,
, QE,然后求出AQ=EQ,再根据角平分线的定义可得∠AQO=∠EQO,然后利用“边角边”证明△AQO和△EQO全等;
QE,然后求出AQ=EQ,再根据角平分线的定义可得∠AQO=∠EQO,然后利用“边角边”证明△AQO和△EQO全等;

 (1)求b+c的值;
(1)求b+c的值; (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.