练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    ①sin2A+cos2A=________，②tanA•cotA=________．

    1    1
    分析：画出直角三角形，根据定义即可证明．
    解答：解：如图：①∵sinA=，cosA=，
    ∴sin2A+cos2A=（）2+（）2===1；
    ②∵tanA=，cotA=，
    ∴tanA•cotA=•=1．
    点评：此题考查了锐角三角函数的定义，只要画出图形即可列式计算．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

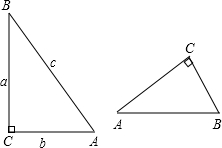    如图，已知在Rt△ABC中，∠C=90°，它的三边长分别为a，b，c，对于同一个锐精英家教网角A的正弦，余弦存在关系式sin2A+cos2A=1试说明．
    解：∵sinA=
     
    ，cosA=
     
    ．
    ∴sin2A+cos2A=
     
    ，
    ∵a2+b2=c2，∴sin2A+cos2A=1．
    （1）在横线上填上适当内容；
    （2）若∠α为锐角，利用（1）的关系式解决下列问题．
    ①若sinα=
    4
    5
    ，求cosα的值；cosα=
    3
    5

    ②若sinα+cosα=1.1，求sinαcosα的值．sinαcosα=0.105．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    下列说法中，正确的是（　　）
    A、在Rt△ABC中，若tanA=
    3
    4
    ，则a=4，b=3
    B、若三角形的三边之比为1：
    		3
    ：2，则三角形是直角三角形
    C、对于锐角α，必有sinα＜cosα
    D、在Rt△ABC中，∠C=90°，则sin2A+cos2B=1

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2012•衡阳）观察下列等式
    ①sin30°=
    1
    2
         cos60°=
    1
    2

    ②sin45°=
    		2
    2
       cos=45°=
    		2
    2

    ③sin60°=
    		3
    2
        cos30°=
    		3
    2

    …
    根据上述规律，计算sin2a+sin2（90°-a）=
    1
    1
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在Rt△ABC中，∠C=90°，下列等式：（1）sin A=sin B；（2）a=c•sin B；（3）sin A=tan A•cos A；（4）sin2A+cos2A=1．其中一定能成立的有（　　）

    查看答案和解析>>

    科目：初中数学 来源：2012年初中毕业升学考试（湖南衡阳卷）数学（解析版） 题型：填空题

    观察下列等式

    ①sin30°=     cos60°=

    ②sin45°=   cos=45°=

    ③sin60°=    cos30°=

    …

    根据上述规律，计算sin2a+sin2（90°﹣a）=        ．

     

    查看答案和解析>>

    同步练习册答案