
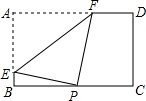
 如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是6-2$\sqrt{5}$≤x≤4.
如图,矩形纸片ABCD中,AB=4,AD=6,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是6-2$\sqrt{5}$≤x≤4. 分析 此题需要运用极端原理求解:①BP最小时,F、D重合,由折叠的性质知:AF=PF,在Rt△PFC中,利用勾股定理可求得PC的长,进而可求得BP的值,即BP的最小值;②BP最大时,E、B重合,根据折叠的性质即可得到AB=BP=34,即BP的最大值为4;根据上述两种情况即可得到BP的取值范围.
解答 解:如图: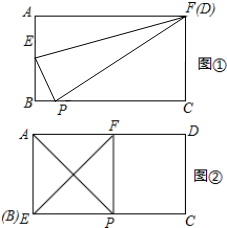
①当F、D重合时,BP的值最小;
根据折叠的性质知:AF=PF=6;
在Rt△PFC中,PF=6,FC=4,则PC=2$\sqrt{5}$;
∴BP=xmin=6-2$\sqrt{5}$;
②当E、B重合时,BP的值最大;根据折叠的性质即可得到AB=BP=4,即BP的最大值为4;
故答案为:6-2$\sqrt{5}$≤x≤4.
点评 此题主要考查的是图形的翻折变换,正确的判断出x的两种极值下F、E点的位置,是解决此题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
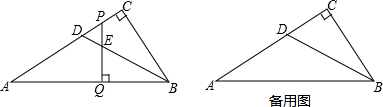
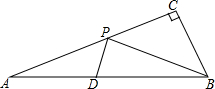 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=2,点D是AB的中点,点P是线段AC上的动点,连接PB,PD,将△BPD沿直线PD翻转,得到△B′PD与△APD重叠部分的面积是△ABP面积的$\frac{1}{4}$时,AP=6-$\sqrt{6}$或$\sqrt{10}$.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=2,点D是AB的中点,点P是线段AC上的动点,连接PB,PD,将△BPD沿直线PD翻转,得到△B′PD与△APD重叠部分的面积是△ABP面积的$\frac{1}{4}$时,AP=6-$\sqrt{6}$或$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,把一张对边平行的长方形ABCD(AD∥BC,AB∥DC)的纸片沿EF折叠后,ED、BC的交点为G,点D、C分别落在D′C′的位置上,若∠EFG=55°,求∠EGF的度数.
如图,把一张对边平行的长方形ABCD(AD∥BC,AB∥DC)的纸片沿EF折叠后,ED、BC的交点为G,点D、C分别落在D′C′的位置上,若∠EFG=55°,求∠EGF的度数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
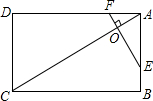 如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.
如图,矩形ABCD中,点O在对角线AC上,EF⊥AC交AB于E点,交AD于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
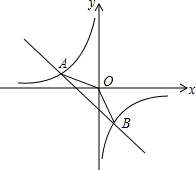 如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,n).
如图,在平面直角坐标系xOy中,一次函数y1=ax+b(a,b为常数,且a≠0)与反比例函数y2=$\frac{m}{x}$(m为常数,且m≠0)的图象交于点A(-2,1)、B(1,n).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )
小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使?ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com