解:(1)∵A(-3,0),
∴OA=3,
∵⊙C的圆心坐标为(3,0),并与x轴交于坐标原点O,
∴⊙C的半径为3,
∴AE长度的最小值为3,最大值为3+3×2=9;
故答案为:3,9;
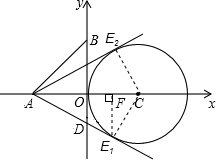
(2)如图,连接CE
1、CE
2,
∵点E运动到点E
1和点E
2时,线段AE所在的直线与⊙C相切,
∴CE
1⊥AE
1,CE
2⊥AE
2,
∵cos∠ACE
1=
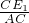
=

=

,
∴∠ACE
1=60°,
过点E
1作E
1F⊥x轴于F,则E
1F=CE
1•sin60°=3×sin60°=3×

=

,
∴△ACE
1的面积=

AC•E
1F=

×6×

=
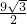
,
同理可得,△ACE
2的面积=
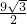
,
∴四边形AE
1CE
2的面积=△ACE
1的面积+△ACE
2的面积=
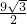
+
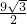
=9

,
由AE
1、AE
2、弧E
1OE
2所围成的图形的面积=四边形AE
1CE
2的面积-扇形CE
1E
2的面积,
=9

-
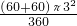
,
=9

-3π;
(3)∵∠ACE
1=60°,
∴∠DAO=90°-ACE
1=90°-60°=30°,
∴OD=AO•tan∠DAO=3tan30°=3×

=

,
∵点A到BD的距离为OA的长度,不变,
∴点D在y轴负半轴时,△ABD的面积取得最大值,
此时BD=OB+OD=3+

,
最大面积为:

×(3+

)×3=
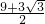
,
在y轴正半轴时,△ABD的面积取得最小值,
时BD=OB-OD=3-

,
最小面积为:

×(3-

)×3=

.
分析:(1)根据动点E在x轴上时,AE取得最小值与最大值解答;
(2)连接CE
1、CE
2,根据圆的切线的定义可得CE
1⊥AE
1,CE
2⊥AE
2,解直角三角形求出∠ACE
1=60°,过点E
1作E
1F⊥x轴于F,利用∠ACE
1的正弦求出E
1F,然后利用三角形的面积求出△ACE
1的面积,同理可得△ACE
2的面积,再根据由AE
1、AE
2、弧E
1OE
2所围成的图形的面积=四边形AE
1CE
2的面积-扇形CE
1E
2的面积,然后列式计算即可得解;
(3)根据直角三角形两锐角互余求出∠DAO=30°,利用∠DAO的正切值求出OD的长度,根据三角形的面积,点D在y轴负半轴时,△ABD的面积取得最大值,在y轴正半轴时,△ABD的面积取得最小值,然后进行计算即可得解,
点评:本题是圆的综合题型,主要考查了圆外一点与圆上各点的距离的最值问题,圆的切线问题,解直角三角形,以及三角形的面积,综合题,但难度不大,(1)(3)确定出最大值与最小值时的点E的位置是解题的关键,(2)根据对称性求出四边形的面积,并表示出围成图形的表示是解题的关键.

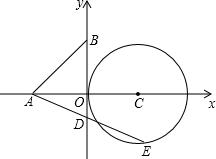 如图,已知A,B两点的坐标分别为(-3,0),(0,3),⊙C的圆心坐标为(3,0),并与x轴交于坐标原点O.若E是⊙C上的一个动点,线段AE与y轴交于点D.
如图,已知A,B两点的坐标分别为(-3,0),(0,3),⊙C的圆心坐标为(3,0),并与x轴交于坐标原点O.若E是⊙C上的一个动点,线段AE与y轴交于点D.
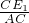 =
= =
= ,
, =
= ,
, AC•E1F=
AC•E1F= ×6×
×6× =
=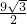 ,
,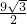 ,
,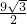 +
+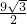 =9
=9 ,
, -
-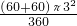 ,
, -3π;
-3π; =
= ,
, ,
, ×(3+
×(3+ )×3=
)×3=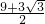 ,
, ,
, ×(3-
×(3- )×3=
)×3= .
.

 名校课堂系列答案
名校课堂系列答案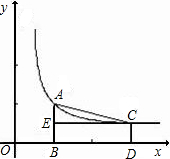 如图,已知A、C两点在双曲线y=
如图,已知A、C两点在双曲线y= (2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是
(2012•福田区二模)如图,已知A、B两点的坐标分别为(-2,0)、(0,1),⊙C的圆心坐标为(0,-1),半径为1.若D是⊙C上的一个动点,射线AD与y轴交于点E,则△ABE面积的最大值是 如图,已知A、B两点的坐标分别为(2
如图,已知A、B两点的坐标分别为(2 如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.
如图,已知M、N两点在正方形ABCD的对角线BD上移动,∠MCN为定角,连接AM、AN,并延长分别交BC、CD于E、F两点,则∠CME与∠CNF在M、N两点移动过程,它们的和是否有变化?证明你的结论.