
����Ŀ���������ϣ���A��ʾ��a����B��ʾ��b����֪a��b����![]() .
.
��1����a��b��ֵ��
��2�����������ϴ���һ��C��ʹ��C��A�ľ�����C��B�ľ����2�������C��ʾ������
��3����С���ϼ״ӵ�A����1����λ����/����ٶ������˶���ͬʱС�����Ҵӵ�B����2����λ����/����ٶ�Ҳ�����˶�����ͬѧ�۲���ֻС�����˶��������Ǹտ�ʼ�˶�ʱ��ԭ��O������һ�ŷ��������������������������ŷ�����ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊt�룮��ס�����ֻС���ϵ�ԭ��ľ������ʱ����Ӧ��ʱ��t��
![]()
���𰸡��ס�����С��ԭ��ľ������ʱ������ʱ��Ϊ![]() ���
���![]() ��
��
��������
(1)���ݷǸ������������a��b��ֵ;
(2)��C������A��B֮��,Ҳ�����ڵ�B���Ҳ�;
(3)��Ҫ��������:���ס�������������˶�,��0��t��3ʱ;���ס�������������˶�,��t>3ʱ.�����ٶȡ�ʱ�䡢����Ĺ�ϵ�г����̲����.
��:(1)��![]() ,
,
��![]() ,
,
���a=-2��b=6;
(2)���C��ʾ������x,
������C��A��B֮��ʱ,x-(-2)=2(6-x),
���x=![]() ;
;
������C��B����Ҳ�ʱ, x-(-2)=2(x-6),
���x=7
��������,��C��ʾ![]() ��7;
��7;
(3)���ס�������������˶�,��0��t��3ʱ,
��ʱOA=2+t,OB��=6-2t,
��ɵ÷���2+t=6-2t,
���t=![]() ;
;
�����������˶�,�������˶�,��t>3ʱ,
��ʱOA=2+t,OB��=2t-6,
��ɵ÷���2+t=2t-6,
���t=8.
��:�ס�����С��ԭ��ľ������ʱ������ʱ��Ϊ![]() ���8��.
���8��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=kx2��6x+3����k�����飨��3����2����1��1��2��3��4�������ȡһ���������������ߵĶԳ�����ֱ��x=1���ҷ�ʱ�ĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ACB�У���ACB=90�㣬��A=30������D��AB�ߵ��е㣮
��1����ͼ1����CD=4������ACB���ܳ���
��2����ͼ2����EΪAC���е㣬���߶�CE��CΪ��ת����˳ʱ����ת60����ʹ��E����F��������BF��CD�ڵ�M������DF��ȡDF���е�N������MN����֤��MN=2CM��
��3����ͼ3����CΪ��ת���Ľ��߶�CD˳ʱ����ת90����ʹ��D����E��������BE��CD��M������DE��ȡDE���е�N�����ӽ�MN���Բ���BD��MN��MC֮��Ĺ�ϵ��ֱ��д�����ϵʽ����֤����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�����ϣ���OΪԭ�㣬��A��Ӧ����Ϊ11����B��Ӧ����Ϊb����C�ڵ�B�Ҳ࣬����Ϊ3����λ���߶�BC���������ƶ���
��1����ͼ1�����߶�BC��O��A����֮���ƶ���ijһλ��ʱ��ǡ�������߶�AC=OB�����ʱb��ֵ��
��2���߶�BC��������������AO�����ƶ��Ĺ����У��Ƿ����AC��OB=![]() AB�������ڣ����ʱ����������b��ֵ���������ڣ�˵�����ɣ�
AB�������ڣ����ʱ����������b��ֵ���������ڣ�˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲��±��������Ĺ��ɣ��ش��������⣺
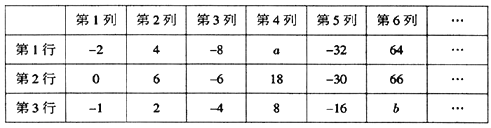
��1����1�еĵ��ĸ���a�Ƕ��٣���3�еĵ�������b�Ƕ�����
��2������1�е�ijһ�е���Ϊc�����2������ͬһ�е���Ϊ������
��3����֪��n�е��������ĺ�Ϊ2562�������1�е�n�е���Ϊx������x��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊӭ�ӡ������������С����죬ij�л�����������A��B�����ͺŵ������䣬ͨ���г����е�֪������3��A���������2��B�������乲��540Ԫ������2��A��������ȹ���3��B������������160Ԫ��
��1��ÿ��A���������B�������������Ԫ��
��2������Ҫ����A��B�����ͺŵ������乲300�����ֱ��ɼס������˽��а�װ��Ҫ����12������ɣ�����ͬʱ���а�װ������֪����A��������İ�װ��ÿ�����װ15�����Ҹ���B��������İ�װ��ÿ�����װ20�����������ұ�ʾ������A�������䲻����150��ʱ�����ͺŵIJ�Ʒ���Դ���ۣ�������B�������䳬��150��ʱ�����ͺŵIJ�Ʒ���Դ���ۣ��������ڹ涨ʱ�����������������ͣ�Ӧ����A�ͺ�B������������ٸ�����ͷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.2 ![]() +3
+3 ![]() =5
=5 ![]()
B.�� ![]() ����1��
����1�� ![]() ��=1
��=1
C.��xy����1�� ![]() xy��2=
xy��2= ![]() xy
xy
D.������a��4��a2=a2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪5̨A�ͻ���һ��IJ�Ʒװ��8���ʣ4����7̨B�ͻ���һ��IJ�Ʒװ��11���ʣ1����ÿ̨A�ͻ�����B�ͻ���һ�������1����Ʒ��
��1����ÿ��װ���ٸ���Ʒ��
��2��3̨A�ͻ�����2̨B�ͻ���һ�����������ٸ���Ʒ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��չУ�����˶���ij�س�����У�������Ϲ���һ�������˶�װ�����г����鷢�֣��ס������̳���ͬ���ļ۸����ͬ��Ʒ�Ƶ�����ӷ���������֪ÿ�ӷ���ÿ�������50Ԫ�����ӷ�����������ķ�����ȣ���Ǣ̸�����̳����Żݷ����ǣ�ÿ����10�ӷ�����1���������̳����Żݷ����ǣ�������ӷ�����80�ף������������ۣ�
(1)ÿ�ӷ���ÿ������ļ۸�ֱ��Ƕ��٣�
(2)��������У���Ϲ���100�ӷ���a���������ú�a��ʽ�ӷֱ��ʾ�������̳������̳�����װ������ķ��ã�
(3)�������DZ��ι�������ĸ����ˣ�����Ϊ���ļ��̳�����ȽϺ��㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com