
【题目】已知5台A型机器一天的产品装满8箱后还剩4个,7台B型机器一天的产品装满11箱后还剩1个,每台A型机器比B型机器一天多生产1个产品.
(1)求每箱装多少个产品.
(2)3台A型机器和2台B型机器一天能生产多少个产品?
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC. 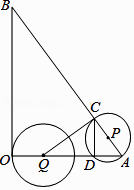
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A表示数a,点B表示数b,已知a、b满足![]() .
.
(1)求a、b的值;
(2)若在数轴上存在一点C,使得C到A的距离是C到B的距离的2倍,求点C表示的数;
(3)若小蚂蚁甲从点A处以1个单位长度/秒的速度向左运动,同时小蚂蚁乙从点B处以2个单位长度/秒的速度也向左运动,丙同学观察两只小蚂蚁运动,在它们刚开始运动时在原点O处放置一颗饭粒,乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动,设运动的时间为t秒.求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,把表示数1的点称为基准点,记作点![]() . 对于两个不同的M和N,若点M、点N到点
. 对于两个不同的M和N,若点M、点N到点![]() 的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数
的距离相等,则称点M与点N互为基准变换点. 例如:图中,点M表示数![]() ,点N表示数3,它们与基准点
,点N表示数3,它们与基准点![]() 的距离都是2个单位长度,点M与点N互为基准变换点.
的距离都是2个单位长度,点M与点N互为基准变换点.

(1)已知点A表示数a,点B表示数b,点A与点B互为基准变换点.
① 若a=0,则b= ;若![]() ,则b= ;
,则b= ;
② 用含a的式子表示b,则b= ;
(2)对点A进行如下操作:先把点A表示的数乘以![]() ,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;
,再把所得数表示的点沿着数轴向左移动3个单位长度得到点B. 若点A与点B互为基准变换点,则点A表示的数是 ;
(3)点P在点Q的左边,点P与点Q之间的距离为8个单位长度.对P、Q两点做如下操作:点P沿数轴向右移动k(k>0)个单位长度得到![]() ,
, ![]() 为
为![]() 的基准变换点,点
的基准变换点,点![]() 沿数轴向右移动k个单位长度得到
沿数轴向右移动k个单位长度得到![]() ,
, ![]() 为
为![]() 的基准变换点,……,依此顺序不断地重复,得到
的基准变换点,……,依此顺序不断地重复,得到![]() ,
, ![]() ,…,
,…, ![]() .
. ![]() 为Q的基准变换点,将数轴沿原点对折后
为Q的基准变换点,将数轴沿原点对折后![]() 的落点为
的落点为![]() ,
, ![]() 为
为的基准变换点, 将数轴沿原点对折后
![]() 的落点为
的落点为![]() ,……,依此顺序不断地重复,得到
,……,依此顺序不断地重复,得到![]() ,
, ![]() ,…,
,…, ![]() .若无论k为何值,
.若无论k为何值, ![]() 与
与![]() 两点间的距离都是4,则n= .
两点间的距离都是4,则n= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,矩形ABCD边AB=6,BC=8,再沿EF折叠,使D点与B点重合,C点的对应点为G,将△BEF绕着点B顺时针旋转,旋转角为a(0°<a<180°),记旋转这程中的三角形为△BE′F′,在旋转过程中设直线E′F′与射钱EF、射线ED分别交于点M、N,当EN=MN时,则FM的长为_____.
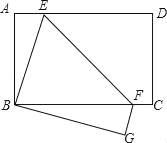
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BC=30,AB=50.点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于E.点M在线段AP上,点N在线段BP上,EM=EN,sin∠EMP= ![]() .
.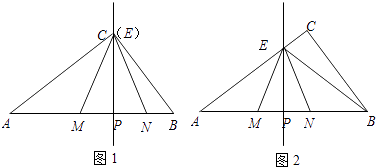
(1)如图1,当点E与点C重合时,求CM的长;
(2)如图2,当点E在边AC上时,点E不与点A,C重合,设AP=x,BN=y,求y关于x的函数关系式,并写出x的取值范围;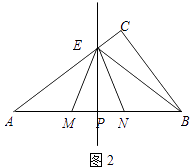
(3)若△AME∽△ENB,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 是直线
是直线![]() 在第一象限内的一个动点
在第一象限内的一个动点
(1)求⊿![]() 的面积
的面积![]() 与
与![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围?
的取值范围?
(2)过点![]() 作
作![]() 轴于点
轴于点![]() , 作
, 作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,是否存在一点
,是否存在一点![]() 使得
使得![]() 的长最小,若存在,求出
的长最小,若存在,求出![]() 的最小值;若不存在,请说明理由 ?
的最小值;若不存在,请说明理由 ?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年度 | 投入技改资金 | 产品成本 |
2014 |
|
|
2015 | 3 | 12 |
2016 | 4 | 9 |
2017 |
| 8 |
(1)分析表中数据,请从一次函数和反比例函数中确定一个函数表示其变化规律,直接写出y与x的函数关系式;
(2)按照这种变化规律,若2018年已投入资金6万元.
①预计2018年每件产品成本比2017年降低多少万元?
②若计划在2018年把每件产品成本降低到5万元,则还需要投入技改资金多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com