
ЁОЬтФПЁПдкRtЁїABCжаЃЌЁЯACB=90ЁуЃЌBC=30ЃЌAB=50ЃЎЕуPЪЧABБпЩЯШЮвтвЛЕуЃЌжБЯпPEЁЭABЃЌгыБпACЛђBCЯрНЛгкEЃЎЕуMдкЯпЖЮAPЩЯЃЌЕуNдкЯпЖЮBPЩЯЃЌEM=ENЃЌsinЁЯEMP= ![]() ЃЎ
ЃЎ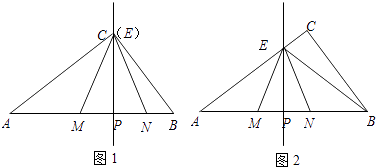
ЃЈ1ЃЉШчЭМ1ЃЌЕБЕуEгыЕуCжиКЯЪБЃЌЧѓCMЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБЕуEдкБпACЩЯЪБЃЌЕуEВЛгыЕуAЃЌCжиКЯЃЌЩшAP=xЃЌBN=yЃЌЧѓyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЛ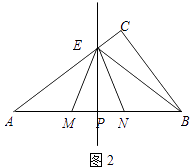
ЃЈ3ЃЉШєЁїAMEЁзЁїENBЃЌЧѓAPЕФГЄЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКЁпЁЯACB=90ЁуЃЌ
ЁрAC= ![]() =
= ![]() =40ЃЌ
=40ЃЌ
ЁпCPЁЭABЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
ЁрCP=24ЃЌ
ЁрCM= ![]() =
= ![]() =26
=26
ЃЈ2ЃЉ
НтЃКЁпsinЁЯEMP= ![]() ЃЌ
ЃЌ
ЁрЩшEP=12aЃЌ
дђEM=13aЃЌPM=5aЃЌ
ЁпEM=ENЃЌ
ЁрEN=13aЃЌPN=5aЃЌ
ЁпЁїAEPЁзЁїABCЃЌ
Ёр ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]()
Ёрx=16aЃЌ
Ёрa= ![]() ЃЌ
ЃЌ
ЁрBP=50Љ16aЃЌ
Ёрy=50Љ21aЃЌ
=50Љ21ЁС ![]() ЃЌ
ЃЌ
=50Љ ![]() xЃЌ
xЃЌ
ЁпЕБEЕугыAЕужиКЯЪБЃЌx=0ЃЎЕБEЕугыCЕужиКЯЪБЃЌx=32ЃЎ
ЁрКЏЪ§ЕФЖЈвхгђЪЧЃКЃЈ0ЃМxЃМ32ЃЉ
ЃЈ3ЃЉ
НтЃКЂйЕБЕуEдкACЩЯЪБЃЌШчЭМ2ЃЌ
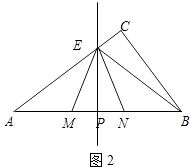
ЩшEP=12aЃЌдђEM=13aЃЌMP=NP=5aЃЌ
ЁпЁїAEPЁзЁїABCЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
ЁрAP=16aЃЌ
ЁрAM=11aЃЌ
ЁрBN=50Љ16aЉ5a=50Љ21aЃЌ
ЁпЁїAMEЁзЁїENBЃЌ
Ёр ![]() =
= ![]()
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
Ёрa= ![]() ЃЌ
ЃЌ
ЁрAP=16ЁС ![]() =22ЃЌ
=22ЃЌ
ЂкЕБЕуEдкBCЩЯЪБЃЌШчЭМЃЈБИгУЭМЃЉЃЌЩшEP=12aЃЌдђEM=13aЃЌMP=NP=5aЃЌ
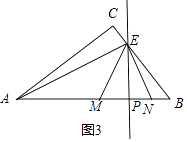
ЁпЁїEBPЁзЁїABCЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
МД ![]() =
= ![]() ЃЌ
ЃЌ
НтЕУBP=9aЃЌ
ЁрBN=9aЉ5a=4aЃЌAM=50Љ9aЉ5a=50Љ14aЃЌ
ЁпЁїAMEЁзЁїENBЃЌ
Ёр ![]() =
= ![]() ЃЌ
ЃЌ
МД ![]() =
= ![]() ЃЌ
ЃЌ
НтЕУa= ![]() ЃЌ
ЃЌ
ЁрAP=50Љ9a=50Љ9ЁС ![]() =42ЃЎ
=42ЃЎ
ЫљвдAPЕФГЄЮЊЃК22Лђ42ЃЎ
ЁОНтЮіЁПЃЈЃЈ1ЃЉБОЬташЯШИљОнвбжЊЬѕМўЕУГіACЕФжЕЃЌдйИљОнCPЁЭABЧѓГіCPЃЌДгЖјЕУГіCMЕФжЕЃЎЃЈ2ЃЉБОЬташЯШИљОнENЃЌИљОнsinЁЯEMP= ![]() ЃЌЩшГіEPЕФжЕЃЌДгЖјЕУГіEMКЭPMЕФжЕЃЌдйЕУГіЁїAEPЁзЁїABCЃЌМДПЩЧѓГі
ЃЌЩшГіEPЕФжЕЃЌДгЖјЕУГіEMКЭPMЕФжЕЃЌдйЕУГіЁїAEPЁзЁїABCЃЌМДПЩЧѓГі ![]() =
= ![]() ЃЌЧѓГіaЕФжЕЃЌМДПЩЕУГіyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧвФмЧѓГіКЏЪ§ЕФЖЈвхгђЃЎЃЈ3ЃЉБОЬташЯШЩшEPЕФжЕЃЌЕУГідђEMКЭMPЕФжЕЃЌШЛКѓЗжЂйЕуEдкACЩЯЪБЃЌИљОнЁїAEPЁзЁїABCЃЌЧѓГіAPЕФжЕЃЌДгЖјЕУГіAMКЭBNЕФжЕЃЌдйИљОнЁїAMEЁзЁїENBЃЌЧѓГіaЕФжЕЃЌЕУГіAPЕФГЄЃЛЂкЕуEдкBCЩЯЪБЃЌИљОнЁїEBPЁзЁїABCCЃЌЧѓГіAPЕФжЕЃЌДгЖјЕУГіAMКЭBNЕФжЕЃЌдйИљОнЁїAMEЁзЁїENBЃЌЧѓГіaЕФжЕЃЌЕУГіAPЕФГЄЃЎ
ЃЌЧѓГіaЕФжЕЃЌМДПЩЕУГіyЙигкxЕФКЏЪ§ЙиЯЕЪНЃЌВЂЧвФмЧѓГіКЏЪ§ЕФЖЈвхгђЃЎЃЈ3ЃЉБОЬташЯШЩшEPЕФжЕЃЌЕУГідђEMКЭMPЕФжЕЃЌШЛКѓЗжЂйЕуEдкACЩЯЪБЃЌИљОнЁїAEPЁзЁїABCЃЌЧѓГіAPЕФжЕЃЌДгЖјЕУГіAMКЭBNЕФжЕЃЌдйИљОнЁїAMEЁзЁїENBЃЌЧѓГіaЕФжЕЃЌЕУГіAPЕФГЄЃЛЂкЕуEдкBCЩЯЪБЃЌИљОнЁїEBPЁзЁїABCCЃЌЧѓГіAPЕФжЕЃЌДгЖјЕУГіAMКЭBNЕФжЕЃЌдйИљОнЁїAMEЁзЁїENBЃЌЧѓГіaЕФжЕЃЌЕУГіAPЕФГЄЃЎ
ЁОПМЕуОЋЮіЁПБОЬтжївЊПМВщСЫЯрЫЦШ§НЧаЮЕФгІгУЕФЯрЙижЊЪЖЕуЃЌашвЊеЦЮеВтИпЃКВтСПВЛФмЕНДяЖЅВПЕФЮяЬхЕФИпЖШЃЌЭЈГЃгУЁАдкЭЌвЛЪБПЬЮяИпгыгАГЄГЩБШР§ЁБЕФдРэНтОіЃЛВтОрЃКВтСПВЛФмЕНДяСНЕуМфЕФОйР§ЃЌГЃЙЙдьЯрЫЦШ§НЧаЮЧѓНтВХФме§ШЗНтД№ДЫЬтЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRtЁїACBжаЃЌЁЯACB=90ЁуЃЌЁЯA=30ЁуЃЌЕуDЪЧABБпЕФжаЕуЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєCD=4ЃЌЧѓЁїACBЕФжмГЄЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌШєEЮЊACЕФжаЕуЃЌНЋЯпЖЮCEвдCЮЊа§зЊжааФЫГЪБеыа§зЊ60ЁуЃЌЪЙЕуEжСЕуFДІЃЌСЌНгBFНЛCDгкЕуMЃЌСЌНгDFЃЌШЁDFЕФжаЕуNЃЌСЌНгMNЃЌЧѓжЄЃКMN=2CMЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌвдCЮЊа§зЊжааФНЋЯпЖЮCDЫГЪБеыа§зЊ90ЁуЃЌЪЙЕуDжСЕуEДІЃЌСЌНгBEНЛCDгкMЃЌСЌНгDEЃЌШЁDEЕФжаЕуNЃЌСЌНгНЛMNЃЌЪдВТЯыBDЁЂMNЁЂMCжЎМфЕФЙиЯЕЃЌжБНгаДГіЦфЙиЯЕЪНЃЌВЛжЄУїЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаМЦЫуе§ШЗЕФЪЧЃЈ ЃЉ
A.2 ![]() +3
+3 ![]() =5
=5 ![]()
B.ЃЈ ![]() ЃЉЃЈ1Љ
ЃЉЃЈ1Љ ![]() ЃЉ=1
ЃЉ=1
C.ЃЈxyЃЉЉ1ЃЈ ![]() xyЃЉ2=
xyЃЉ2= ![]() xy
xy
D.ЉЃЈЉaЃЉ4ЁТa2=a2
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ5ЬЈAаЭЛњЦївЛЬьЕФВњЦЗзАТњ8ЯфКѓЛЙЪЃ4ИіЃЌ7ЬЈBаЭЛњЦївЛЬьЕФВњЦЗзАТњ11ЯфКѓЛЙЪЃ1ИіЃЌУПЬЈAаЭЛњЦїБШBаЭЛњЦївЛЬьЖрЩњВњ1ИіВњЦЗЃЎ
ЃЈ1ЃЉЧѓУПЯфзАЖрЩйИіВњЦЗЃЎ
ЃЈ2ЃЉ3ЬЈAаЭЛњЦїКЭ2ЬЈBаЭЛњЦївЛЬьФмЩњВњЖрЩйИіВњЦЗЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯжДњЛЅСЊЭјММЪѕЕФЙуЗКгІгУЃЌДпЩњСЫПьЕнаавЕЕФИпЫйЗЂеЙЃЎаЁУїМЦЛЎИјХѓгбПьЕнвЛВПЗжЮяЦЗЃЌОСЫНтгаМзЁЂввСНМвПьЕнЙЋЫОБШНЯКЯЪЪЃЎМзЙЋЫОБэЪОЃКПьЕнЮяЦЗВЛГЌЙ§1ЧЇПЫЕФЃЌАДУПЧЇПЫ22дЊЪеЗбЃЛГЌЙ§1ЧЇПЫЃЌГЌЙ§ЕФВПЗжАДУПЧЇПЫ15дЊЪеЗбЃЎввЙЋЫОБэЪОЃКАДУПЧЇПЫ16дЊЪеЗбЃЌСэМгАќзАЗб3дЊЃЎЩшаЁУїПьЕнЮяЦЗxЧЇПЫЃЎ
(1)ЧыЗжБ№аДГіМзЁЂввСНМвПьЕнЙЋЫОПьЕнИУЮяЦЗЕФЗбгУy(дЊ)гыx(ЧЇПЫ)жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
(2)аЁУїбЁдёФФМвПьЕнЙЋЫОИќЪЁЧЎЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪ§жсЩЯЃЌAЁЂBСНЕуБэЪОЕФЪ§aЃЌbТњзу|aЉ6|+ЃЈb+12ЃЉ2=0
ЃЈ1ЃЉa=ЁЁ ЁЁЃЌb=ЁЁ ЁЁЃЛ
ЃЈ2ЃЉШєаЁЧђMДгAЕуЯђИКАыжсдЫЖЏЁЂаЁЧђNДгBЕуЯђе§АыжсдЫЖЏЃЌСНЧђЭЌЪБГіЗЂЃЌаЁЧђMдЫЖЏЕФЫйЖШЮЊУПУы2ИіЕЅЮЛЃЌЕБMдЫЖЏЕНOBЕФжаЕуЪБЃЌNЕувВЭЌЪБдЫЖЏЕНOAЕФжаЕуЃЌдђаЁЧђNЕФЫйЖШЪЧУПУыЁЁ ЁЁИіЕЅЮЛЃЛ
ЃЈ3ЃЉШєаЁЧђMЁЂNБЃГжЃЈ2ЃЉжаЕФЫйЖШЃЌЗжБ№ДгAЁЂBСНЕуЭЌЪБГіЗЂЃЌОЙ§ЁЁ ЁЁУыКѓСНИіаЁЧђЯрОрСНИіЕЅЮЛГЄЖШЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКEЪЧБпГЄЮЊ1ЕФе§ЗНаЮABCDЕФЖдНЧЯпBDЩЯвЛЕуЃЌЧвBE=BCЃЌPЮЊCEЩЯШЮвтвЛЕуЃЌPQЁЭBCгкЕуQЃЌPRЁЭBEгкЕуRЃЌдђPQ+PRЕФжЕЪЧЃЈ ЃЉ 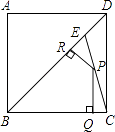
A.![]()
B.![]()
C.![]()
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊЗЂеЙаЃдАзуЧђдЫЖЏЃЌФГЯиГЧЧјЫФаЃОіЖЈСЊКЯЙКТђвЛХњзуЧђдЫЖЏзАБИЃЌЪаГЁЕїВщЗЂЯжЃКМзЁЂввСНЩЬГЁвдЭЌбљЕФМлИёГіЪлЭЌжжЦЗХЦЕФзуЧђЖгЗўКЭзуЧђЃЌвбжЊУПЬзЖгЗўБШУПИізуЧђЖр50дЊЃЌСНЬзЖгЗўгыШ§ИізуЧђЕФЗбгУЯрЕШЃЎОЧЂЬИЃЌМзЩЬГЁЕФгХЛнЗНАИЪЧЃКУПЙКТђ10ЬзЖгЗўЃЌЫЭ1ИізуЧђЃЛввЩЬГЁЕФгХЛнЗНАИЪЧЃКШєЙКТђЖгЗўГЌЙ§80ЬзЃЌдђЙКТђзуЧђДђАЫелЃЎ
(1)УПЬзЖгЗўКЭУПИізуЧђЕФМлИёЗжБ№ЪЧЖрЩйЃП
(2)ШєГЧЧјЫФаЃСЊКЯЙКТђ100ЬзЖгЗўКЭaИізуЧђЃЌЧыгУКЌaЕФЪНзгЗжБ№БэЪОГіЕНМзЩЬГЁКЭввЩЬГЁЙКТђзАБИЫљашЕФЗбгУЃЎ
(3)МйШчФуЪЧБОДЮЙКТђШЮЮёЕФИКд№ШЫЃЌФуШЯЮЊЕНФФМвЩЬГЁЙКТђБШНЯКЯЫуЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЭХЮЏОйаавдЁАЮвЕФжаЙњУЮЁБЮЊжїЬтЕФжЊЪЖОКШќЃЌМзЁЂввСНЫљбЇаЃЕФВЮШќШЫЪ§ЯрЕШЃЌБШШќНсЪјКѓЃЌЗЂЯжбЇЩњГЩМЈЗжБ№ЮЊ![]() ЗжЃЌ
ЗжЃЌ![]() ЗжЃЌ
ЗжЃЌ![]() ЗжЃЌ
ЗжЃЌ![]() ЗжЃЌВЂИљОнЭГМЦЪ§ОнЛцжЦСЫШчЯТВЛЭъећЕФЭГМЦЭМБэЃК ЁЁ
ЗжЃЌВЂИљОнЭГМЦЪ§ОнЛцжЦСЫШчЯТВЛЭъећЕФЭГМЦЭМБэЃК ЁЁ
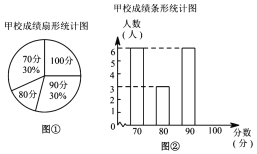
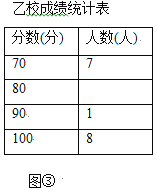
ЃЈ1ЃЉввбЇаЃЕФВЮШќШЫЪ§ЪЧ ШЫЃЛ
ЃЈ2ЃЉдкЭМЂйжаЃЌЁА![]() ЗжЁБЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЮЊЁЁЁЁЁЁЃЛ
ЗжЁБЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЮЊЁЁЁЁЁЁЃЛ
ЃЈ3ЃЉЧыФуНЋЭМЂкВЙГфЭъећЃЛ
ЃЈ4ЃЉЧѓвваЃГЩМЈЕФЦНОљЗжЃЛ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com