
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 是直线
是直线![]() 在第一象限内的一个动点
在第一象限内的一个动点
(1)求⊿![]() 的面积
的面积![]() 与
与![]() 的函数解析式,并写出自变量
的函数解析式,并写出自变量![]() 的取值范围?
的取值范围?
(2)过点![]() 作
作![]() 轴于点
轴于点![]() , 作
, 作![]() 轴于点
轴于点![]() ,连接
,连接![]() ,是否存在一点
,是否存在一点![]() 使得
使得![]() 的长最小,若存在,求出
的长最小,若存在,求出![]() 的最小值;若不存在,请说明理由 ?
的最小值;若不存在,请说明理由 ?

【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 的最小值为
的最小值为![]()
【解析】本题的⑴问直接根据坐标来表示⊿![]() 的底边和底边上的高,利用三角形的面积公式得出函数解析式;
的底边和底边上的高,利用三角形的面积公式得出函数解析式;
本题的⑵抓住四边形![]() 是矩形,矩形的对角线相等即
是矩形,矩形的对角线相等即![]() ,从而把
,从而把![]() 转化到
转化到![]() 上来解决,当
上来解决,当![]() 的端点
的端点![]() 运动到
运动到![]() 时
时![]() 最短,以此为切入点,问题可获得解决.
最短,以此为切入点,问题可获得解决.
⑴.∵![]() 的坐标为
的坐标为![]() ,
,![]() 是直线
是直线![]() 在第一象限的一个动点,且
在第一象限的一个动点,且![]() 轴.
轴.
∴![]() ,
,![]()
∴![]() 整理得:
整理得:![]()
自变量![]() 的取值范围是:
的取值范围是:![]()
⑵. 存在一点![]() 使得
使得![]() 的长最小.
的长最小.
求出直线![]() 与
与![]() 轴交点的坐标为
轴交点的坐标为![]() , 与
, 与![]() 轴交点的坐标为
轴交点的坐标为![]()
∴![]() ∴
∴![]()
根据勾股定理计算:![]() .
.
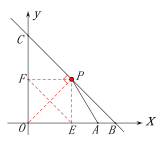
∵![]() 轴,
轴, ![]() 轴,
轴,![]() 轴
轴![]()
![]() 轴
轴
∴![]()
∴四边形![]() 是矩形 ∴
是矩形 ∴![]()
当![]() 的端点
的端点![]() 运动到
运动到![]() (实际上点
(实际上点![]() 恰好是
恰好是![]() 的中点)时
的中点)时
的![]() 最短(垂线段最短)(见示意图)
最短(垂线段最短)(见示意图)
又∵![]() ∴
∴![]() 点为线段
点为线段![]() 中点(三线合一)
中点(三线合一)
∴ ![]() (注:也可以用面积方法求解)
(注:也可以用面积方法求解)
∴![]() 即
即![]() 的最小值为
的最小值为![]()


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】已知数轴上,点O为原点,点A对应的数为11,点B对应的数为b,点C在点B右侧,长度为3个单位的线段BC在数轴上移动,
(1)如图1,当线段BC在O,A两点之间移动到某一位置时,恰好满足线段AC=OB,求此时b的值;
(2)线段BC在数轴上沿射线AO方向移动的过程中,是否存在AC﹣OB=![]() AB?若存在,求此时满足条件的b的值;若不存在,说明理由.
AB?若存在,求此时满足条件的b的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知5台A型机器一天的产品装满8箱后还剩4个,7台B型机器一天的产品装满11箱后还剩1个,每台A型机器比B型机器一天多生产1个产品.
(1)求每箱装多少个产品.
(2)3台A型机器和2台B型机器一天能生产多少个产品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上,A、B两点表示的数a,b满足|a﹣6|+(b+12)2=0
(1)a= ,b= ;
(2)若小球M从A点向负半轴运动、小球N从B点向正半轴运动,两球同时出发,小球M运动的速度为每秒2个单位,当M运动到OB的中点时,N点也同时运动到OA的中点,则小球N的速度是每秒 个单位;
(3)若小球M、N保持(2)中的速度,分别从A、B两点同时出发,经过 秒后两个小球相距两个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( ) 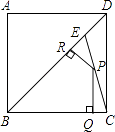
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒.
![]()
(1)写出数轴上点B表示的数 ,点P表示的数 (用含t的代数式表示);
(2)动点H从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、H同时出发,问点P运动多少秒时追上点H?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展校园足球运动,某县城区四校决定联合购买一批足球运动装备,市场调查发现:甲、乙两商场以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多50元,两套队服与三个足球的费用相等.经洽谈,甲商场的优惠方案是:每购买10套队服,送1个足球;乙商场的优惠方案是:若购买队服超过80套,则购买足球打八折.
(1)每套队服和每个足球的价格分别是多少?
(2)若城区四校联合购买100套队服和a个足球,请用含a的式子分别表示出到甲商场和乙商场购买装备所需的费用.
(3)假如你是本次购买任务的负责人,你认为到哪家商场购买比较合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为![]()
(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCB1中,AB=1,AB与直线l的夹角为30°,延长CB1交直线l于点A1 , 作正方形A1B1C1B2 , 延长C1B2交直线l于点A2 , 作正方形A2B2C2B3 , 延长C2B3交直线l于点A3 , 作正方形A3B3C3B4 , …,依此规律,则A2016A2017= . 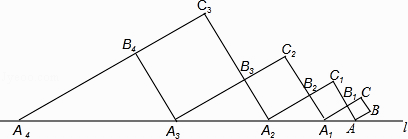
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com