

分析 (1)如图1,利用等腰三角形的性质得∠DCA=∠ADC,CE=AE,再利用CF∥AB得到∠ECF=∠EAD,则∠DCA=∠ECF,于是根据等腰三角形的判定方法可得AD=CF,所以四边形ADCF为平行四边形,
加上DA=DC可判断四边形ADCF是菱形;
(2)如图2,先证明△ADC为等边三角形得到AC=AD=CD,∠ACD=60°,再利用菱形的性质可得AC=AD=DC=CF=AF,然后证明BD=CD即可.
解答 解:(1)证明:如图1,
∵AD=CD,DE⊥AC,
∴∠DCA=∠ADC,CE=AE,
∵CF∥AB,
∴∠ECF=∠EAD,
∴∠DCA=∠ECF,
即CE平分∠DCF,
而CE⊥DF,
∴CD=CF,
∴AD=CF,
∴AD∥CF,
∴四边形ADCF为平行四边形,
而DA=DC,
∴四边形ADCF是菱形;
(2)如图2,∵∠ACB=90°,∠B=30°,
∴∠BAC=60°,
而DA=DC,
∴△ADC为等边三角形,
∴AC=AD=CD,∠ACD=60°,
∵四边形ADCF为菱形,
∴AC=AD=DC=CF=AF,
∵∠B=∠DCB=30°,
∴BD=CD,
∴AC=AD=DC=CF=AF=BD.
点评 本题考查了菱形的判定与性质:菱形的中点四边形是矩形(对角线互相垂直的四边形的中点四边形定为矩形,对角线相等的四边形的中点四边形定为菱形).;菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
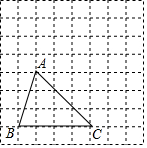 三角形ABC在正方形网格中的位置如图所示,网格中每个小方格的边长为1个单位长度,请根据下列提示作图
三角形ABC在正方形网格中的位置如图所示,网格中每个小方格的边长为1个单位长度,请根据下列提示作图查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com