
【题目】如图,在四边形ABCD的外侧,以四边形的边为边分别作四个小正方形,连接相邻的两个顶点,得到四个阴影三角形,则这四个阴影三角形的面积a、b、c、d满足( ) 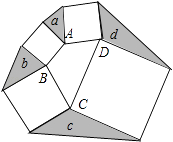
A.a+b=c+d
B.a2+b2=c2+d2
C.a+c=b+d
D.a2+c2=b2+d2
【答案】C
【解析】解:如图,以△ABC的边为边分别正方形ABDE,正方形ACHG. 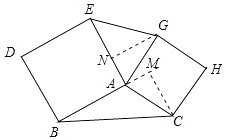
∵S△AEG= ![]() AEGN=
AEGN= ![]() AEAGsin∠EAG,
AEAGsin∠EAG,
S△ACB= ![]() ABCM=
ABCM= ![]() ABACsin∠CAM,
ABACsin∠CAM,
∵AB=AE,AC=AG,
∠EAG+∠BAC=180°,∠CAM+∠BAC=180°,
∴∠EAG=∠CAM,
∴S△AEG=S△ABC ,
如图1中,连接AC、BD.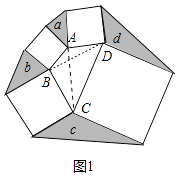
由上面的结论可知,S△ABD=a,S△BCD=c,S△ABC=b,S△ADC=d,
∵S四边形ABCD=a+c=b+d,
∴a+c=b+d,
故选C.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


科目:初中数学 来源: 题型:
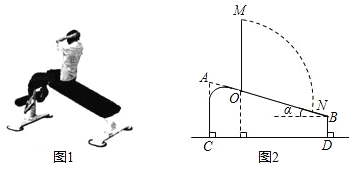
【题目】图①是小明在健身器材上进行仰卧起坐锻炼时的情景,图②是小明锻炼时上半身由ON位置运动到与地面垂直的OM位置时的示意图.已知AC=0.66米,BD=0.26米,α=20°.(参考数据:sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)
(1)求AB的长(精确到0.01米);
(2)若测得ON=0.8米,试计算小明头顶由N点运动到M点的路径![]() 的长度.(结果保留π)
的长度.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
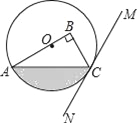
【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两点在数轴上的位置如图所示,其中点A对应的有理数为-4,且AB=10。动点P从点A出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒(t>0)。
(1)当t=1时,AP的长为 , 点P表示的有理数为;
(2)当PB=2时,求t的值;
(3)M为线段AP的中点,N为线段PB的中点. 在点P运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
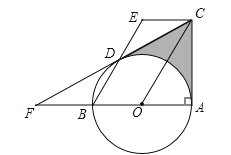
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班将举行“防溺水安全知识竞赛”活动,班主任安排班长购买奖品,下面是班长买回奖品时与班主任的对话情况:
班长:买了两种不同的奖品共50件,单价分别为3元和5元,我领了200元,现在找回35元
班主任:你肯定搞错了!
班长:哦!我把自己口袋里的15元一起当作找回的钱款了.
班主任:这就对了!
请根据上面的信息,解决下列问题:
(1)计算两种奖品各买了多少件?
(2)请你解释:班长为什么不可能找回35元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正五边形ABCDE的边BC,CD上的点,且BM=CN,AM交BN于点P,则∠APN的度数为( ) 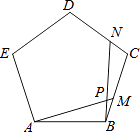
A.120°
B.118°
C.110°
D.108°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com