
| A. | (-b+1,a+1) | B. | (-a,-b+2) | C. | (b-1,-a+1) | D. | (a,b) |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
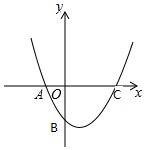 设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.
设抛物线y=$\frac{\sqrt{3}}{2}$(x+1)(x-2)与x轴交于A、C两点(点A在点C的左边),与y轴交于点B.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
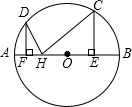 如图,AB是⊙O的直径,C、D是⊙O上的两点,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F、H为EF上的任意一点,若AB=10,CE=4,DF=3,则CH+DH的最小值是7$\sqrt{2}$.
如图,AB是⊙O的直径,C、D是⊙O上的两点,过点C作CE⊥AB于点E,过点D作DF⊥AB于点F、H为EF上的任意一点,若AB=10,CE=4,DF=3,则CH+DH的最小值是7$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
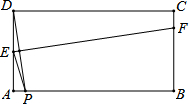 如图,在矩形ABCD中,AB=2,AD=1,点P在线段AB上运动,现将纸片折叠,使点D与点P重台,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原设四边形EPFD的面积为S,当四边形EPFD为菱形时,请写出S的取值范围1≤S≤$\frac{5}{4}$.
如图,在矩形ABCD中,AB=2,AD=1,点P在线段AB上运动,现将纸片折叠,使点D与点P重台,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原设四边形EPFD的面积为S,当四边形EPFD为菱形时,请写出S的取值范围1≤S≤$\frac{5}{4}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
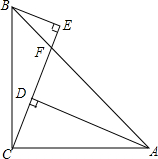 如图,AD=CE=24,BC=25,BE∥AD.BF:AF=7:24,给出下列结论:
如图,AD=CE=24,BC=25,BE∥AD.BF:AF=7:24,给出下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
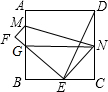 如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )
如图所示,将边长为1cm的正方形纸片ABCD折叠,使点D落在BC上,对应点为E,点A对应点为F,EF交AB于G点,折痕为MN,连接DE,NG,则下列结论正确的是:①∠MNE=∠NMB;②∠DEC=∠DEG;③MN=DE;④△BEG的周长为定值.其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
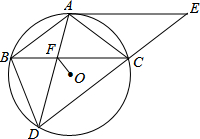 如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.
如图,△ABC内接于⊙O,AB=AC,BD为⊙O的弦,且AB∥CD,过点A作⊙O的切线AE与DC的延长线交于点E,AD与BC交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (1,0) | B. | (3,0) | C. | (-3,0) | D. | (0,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com